数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究C++ 中的二叉树倾斜
假设我们有一个二叉树的根节点，任务是找到并返回每个节点的倾斜度之和。
二叉树的**倾斜度**是指通过在每一层找到左子树和右子树中子节点的绝对差来构建二叉树。在某一层，如果节点没有子节点，我们只需用零替换该节点来计算倾斜度。
示例
输入
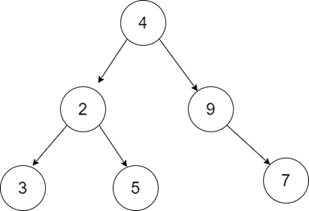
输出：15
解释：找到给定二叉树每一层的倾斜度，
节点 3 的倾斜度 = 0
节点 5 的倾斜度 = 0
节点 7 的倾斜度 = 0
节点 2 的倾斜度 = abs(3-5)= 2
节点 9 的倾斜度 = abs(0-7)= 7
节点 4 的倾斜度 = abs((3+5+2)- (9+7))= 6
所有节点的倾斜度之和 = 2+7+6= 15
解决此问题的方法
解决此特定问题的一种简单方法是使用后序广度优先搜索遍历。
在遍历二叉树时，我们将尝试找到其左子树然后是右子树的所有节点的总和。找到总和后，我们将通过计算其左子树和右子树总和的绝对差来找到所有节点的倾斜度。
- 取一个二叉树作为输入。
- 一个整数函数 sumNodes(treenode*node) 获取树的根节点并返回左子树和右子树的总和。
- 一个整数函数 findTilt(treenode*root) 获取根节点作为输入参数并返回所有节点的倾斜度之和。
示例
#include<iostream>
using namespace std;
struct treenode {
int data;
treenode * left;
treenode * right;
};
struct treenode * createNode(int d) {
struct treenode * root = new treenode;
root -> data = d;
root -> left = NULL;
root -> right = NULL;
return root;
}
int sumNodes(treenode * root, int & sum) {
if (root == NULL) return 0;
int lsum = sumNodes(root -> left, sum);
int rsum = sumNodes(root -> right, sum);
sum += abs(lsum - rsum);
return lsum + rsum + root -> data;
}
int findTilt(treenode * root) {
int sum = 0;
if (root == NULL) {
return 0;
}
sumNodes(root, sum);
return sum;
}
int main() {
struct treenode * root = NULL;
root = createNode(4);
root -> left = createNode(2);
root -> right = createNode(9);
root -> left -> right = createNode(5);
root -> left -> left = createNode(3);
root -> right -> right = createNode(7);
cout << findTilt(root) << endl;
return 0;
}运行以上代码将生成以下输出：
输出
15
在给定的二叉树中，树每一层所有节点的倾斜度之和为 15。
更新于： 2021年2月23日
249 次查看
广告