数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究C++ 中验证二叉树节点
假设我们有 n 个二叉树节点，编号从 0 到 n - 1，其中节点 I 有两个子节点 leftChild[i] 和 rightChild[i]，我们必须在仅当所有给定节点恰好形成一个有效的二叉树时才说真。当节点 i 没有左子节点时，leftChild[i] 将等于 -1，右子节点也类似。我们必须记住，节点没有值，并且我们只在此问题中使用节点编号。因此，如果输入类似于 -
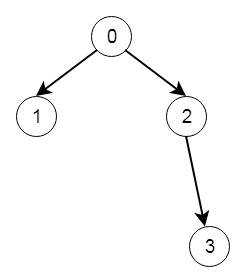
那么输出将为真。
为了解决这个问题，我们将遵循以下步骤 -
定义一个名为 dfs 的方法，它将接收 leftChild、rightChild 和 visited
如果节点 n 已被访问，则返回 false
将节点 n 插入到 visited 集合中
设置 ret := true
如果 n 的 leftChild 不为 -1，则 ret := ret AND dfs(leftChild[node], leftChild, rightChild, visited)
如果 n 的 rightChild 不为 -1，则 ret := ret AND dfs(rightChild[node], leftChild, rightChild, visited)
返回 ret
主方法将如下所示 -
ret := dfs(0, leftChild, rightChild, visited)
设置 allVisited := false
对于 I 范围从 0 到 n – 1
如果 i 未被访问，则返回 false
返回 ret
示例（C++）
让我们看看以下实现以更好地理解 -
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
bool dfs(int node, vector <int>& leftChild, vector <int>& rightChild, set <int>& visited){
if(visited.count(node)) return false;
visited.insert(node);
bool ret = true;
if(leftChild[node] != -1){
ret &= dfs(leftChild[node], leftChild, rightChild, visited);
}
if(rightChild[node] != -1){
ret &= dfs(rightChild[node], leftChild, rightChild, visited);
}
return ret;
}
bool validateBinaryTreeNodes(int n, vector<int>& leftChild, vector<int>& rightChild) {
set <int> visited;
bool ret = dfs(0, leftChild, rightChild, visited);
bool allVisited = true;
for(int i = 0; i < n; i++){
if(!visited.count(i))return false;
}
return ret;
}
};
main(){
vector<int> v1 = {1,-1,3,-1}, v2 = {2,-1,-1,-1};
Solution ob;
cout << (ob.validateBinaryTreeNodes(4, v1, v2));
}输入
4 [1,-1,3,-1] [2,-1,-1,-1]
输出
1
更新于: 2020-04-29
319 次浏览
广告