数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法学研究C++中二叉树完整节点计数（迭代和递归）
给定一个二叉树，任务是使用迭代和递归方法计算二叉树中完整节点的数量。完整节点是指同时具有左右两个子节点，且子节点均不为空的节点。请注意，在完整节点中，我们只考虑恰好有两个子节点的节点。
二叉树是一种用于数据存储的特殊数据结构。二叉树有一个特殊条件，即每个节点最多可以有两个子节点。二叉树结合了有序数组和链表的优点，搜索速度与排序数组一样快，插入或删除操作速度与链表一样快。非叶子节点也称为父节点，因为它们有超过0个子节点，但少于两个子节点。
二叉树的结构如下所示：
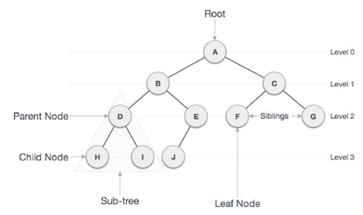
例如
输入：
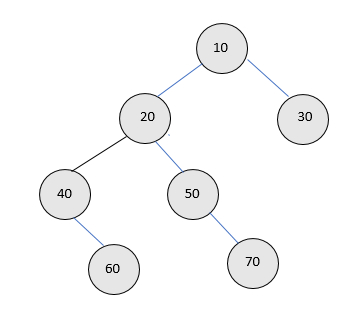
输出：计数为2
解释：在给定的树中，有2个节点（即10和20）恰好有两个子节点或完整节点，其他节点只有一个子节点或没有子节点。
迭代法
下面程序中使用的方法如下：
创建一个包含数据部分、左指针和右指针的节点结构。
创建一个函数，用于将节点插入二叉树。
创建一个函数来计算完整节点。
在函数内部，检查IF !node，则返回，因为树中没有节点。
声明一个临时变量count来存储完整节点的数量
创建一个队列类型变量，例如qu
将节点压入队列中，例如qu.push(node)
循环，直到!qu.empty()
创建一个临时变量，例如Node类型的temp，并将其初始化为queue.front()
使用qu.pop()弹出元素
检查IF (!temp->left AND temp->right)，则将count加1
检查IF (temp->left != NULL)，则执行qu.push(temp->left)
检查IF (temp->right != NULL)，则qu.push(temp->right)
返回count
打印结果。
示例
// Iterative program to count full nodes
#include <iostream>
#include <queue>
using namespace std;
struct Node{
int data;
struct Node* left, *right;
};
// Function to count the full Nodes in a binary tree
int fullcount(struct Node* node){
// Check if tree is empty
if (!node){
return 0;
}
queue<Node *> myqueue;
// traverse using level order traversing
int result = 0;
myqueue.push(node);
while (!myqueue.empty()){
struct Node *temp = myqueue.front();
myqueue.pop();
if (temp->left && temp->right){
result++;
}
if (temp->left != NULL){
myqueue.push(temp->left);
}
if (temp->right != NULL){
myqueue.push(temp->right);
}
}
return result;
}
struct Node* newNode(int data){
struct Node* node = new Node;
node->data = data;
node->left = node->right = NULL;
return (node);
}
int main(void){
struct Node *root = newNode(10);
root->left = newNode(20);
root->right = newNode(30);
root->left->left = newNode(40);
root->left->right = newNode(50);
root->left->left->right = newNode(60);
root->left->right->right = newNode(70);
cout <<"count is: "<<fullcount(root);
return 0;
}输出
如果运行上述代码，我们将得到以下输出：
count is: 2
递归法
下面程序中使用的方法如下：
创建一个包含数据部分、左指针和右指针的节点结构。
创建一个函数，用于将节点插入二叉树。
创建一个函数来计算完整节点。
在函数内部，检查IF !node，则返回，因为树中没有节点。
声明一个临时变量count来存储完整节点的数量
检查IF (root->left AND root->right)，则将count加1
设置count = count + 递归调用此函数(root->left) + 递归调用此函数(root->right)
返回count
打印结果。
示例
// Recursive program to count full nodes
#include <iostream>
using namespace std;
struct Node{
int data;
struct Node* left, *right;
};
// Function to get the count of full Nodes
int fullcount(struct Node* root){
if (root == NULL){
return 0;
}
int result = 0;
if (root->left && root->right){
result++;
}
result += (fullcount(root->left) +
fullcount(root->right));
return result;
}
struct Node* newNode(int data){
struct Node* node = new Node;
node->data = data;
node->left = node->right = NULL;
return (node);
}
int main(){
struct Node *root = newNode(10);
root->left = newNode(20);
root->right = newNode(30);
root->left->left = newNode(40);
root->left->right = newNode(50);
root->left->left->right = newNode(60);
root->left->right->right = newNode(70);
cout <<"count is: "<<fullcount(root);
return 0;
}输出
如果运行上述代码，我们将得到以下输出：
count is: 2
1K+浏览量
