数据结构
网络
关系数据库管理系统(RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学C++二叉树中非叶子节点的计数
给定一个二叉树，任务是计算二叉树中非叶子节点的数量。
二叉树是一种用于数据存储的特殊数据结构。二叉树有一个特殊条件，即每个节点最多可以有两个子节点。二叉树结合了有序数组和链表的优点，搜索速度像排序数组一样快，插入或删除操作像链表一样快。非叶子节点也称为父节点，因为它们具有多于0个子节点且少于2个子节点。
二叉树的结构如下所示：
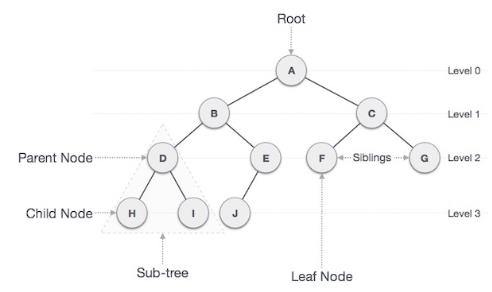
例如
输入：
输出：非叶子节点数量为：3
解释：在给定的树中，27、14和35是非叶子节点，因为它们具有多于0个子节点且少于2个子节点。
下面程序中使用的算法如下：
创建二叉树结构，包含指向左节点的指针、指向右节点的指针以及存储在节点中的数据部分。
创建一个函数，每当调用此函数时都会插入一个节点。为此，将数据插入新节点，并将新节点的左右指针设置为NULL，然后返回该节点。
创建一个递归函数，用于计算二叉树中非叶子节点的数量。
- 检查根节点是否为NULL，或者根节点的左子节点和右子节点是否为NULL，如果是，则返回0。
- 返回1 + 对此函数的递归调用（使用左指针）+ 对此函数的递归调用（使用右指针）。
打印计数。
示例
#include <iostream>
using namespace std;
// Node's structure
struct Node {
int data;
struct Node* left;
struct Node* right;
};
// To define the new node
struct Node* newNode(int data){
struct Node* node = new Node;
node->data = data;
node->left = node->right = NULL;
return (node);
}
// Count the non leaf nodes.
int nonleaf(struct Node* root){
if (root == NULL || (root->left == NULL && root->right == NULL)){
return 0;
}
return 1 + nonleaf(root->left) + nonleaf(root->right);
}
// Main function
int main(){
struct Node* root = newNode(10);
root->left = newNode(21);
root->right = newNode(33);
root->left->left = newNode(48);
root->left->right = newNode(51);
cout << nonleaf(root);
return 0;
}输出
如果运行以上代码，将生成以下输出：
count of non-leaf nodes is: 2
更新于：2020年5月15日
2K+ 次浏览
广告