数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究使用C++中一个栈从左到右打印二叉树的叶子节点
程序应该从左到右打印二叉树的叶子节点，但挑战在于只能使用一个栈。
通过push()函数插入二叉树的节点，并通过pop()操作显示叶子节点。
叶子节点是左右指针都为NULL的末端节点，这意味着该节点不是父节点。
示例
Input : 12 21 32 41 59 33 70 Output : 41 59 33 70
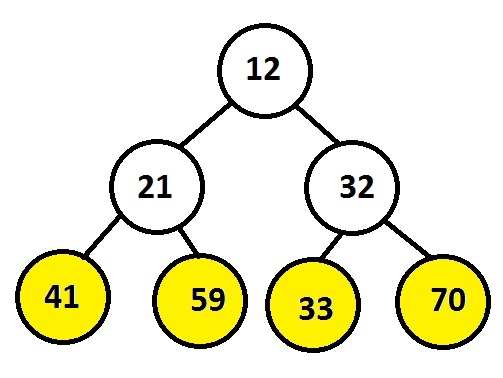
栈是一种后进先出(LIFO)的数据结构，其中顶部指针指向最后插入的元素，因此叶子节点将最后插入栈中，并且根据栈的结构，它们将在任何其他节点之前从栈中弹出或移除。
下面的代码显示了使用STL的C++算法实现。
算法
START Step 1 -> create node variable of type structure Declare int data Declare pointer of type node using *left, *right Step 2 -> create function for inserting node with parameter as val Declare node variable of node using malloc Set node->data = val Set node->left = node->right = NULL return node step 3 -> Declare Function void leaf(Node *ptr) create vector stack<Node*>stck Loop While 1 IF ptr Stck.push(ptr) Ptr = ptr->left Else IF (stck.empty()) Break Else IF (stck.top()->right == NULL) Set ptr = stck.top() Set stck.pop() IF ptr->left = NULL Print ptr->data End Loop While ptr == stck.top()->right Set ptr = stck.top() Call stck.pop() IF stck.empty() Break End IF !stck.empty() Set ptr = tck.top()->right Else Set ptr = NULL EndIF End End End Step 4-> In main() Call New passing value user want to insert as Node* root = New(12) Call leaf(root) STOP
示例
#include <bits/stdc++.h>
using namespace std;
// Structure of a node
struct Node {
Node* left;
Node* right;
int data;
};
//Function to create a new node
Node* New(int val) {
Node* node = new Node();
node->left = node->right = NULL;
node->data = val;
return node;
}
// leaf node using stack
void leaf(Node* ptr) {
// stack that will store nodes
stack<Node*> stck;
while (1) {
if (ptr) {
stck.push(ptr);
ptr = ptr->left;
} else {
if (stck.empty())
break;
else {
if (stck.top()->right == NULL) {
ptr = stck.top();
stck.pop();
// Print the leaf node
if (ptr->left == NULL)
printf("%d ", ptr->data);
}
while (ptr == stck.top()->right) {
ptr = stck.top();
stck.pop();
if (stck.empty())
break;
}
if (!stck.empty())
ptr = stck.top()->right;
else
ptr = NULL;
}
}
}
}
int main() {
printf("leaf nodes at end level are : ");
Node* root = New(12);
root->left = New(21);
root->right = New(32);
root->left->left = New(41);
root->left->right = New(59);
root->right->left = New(33);
root->right->right = New(70);
leaf(root);
return 0;
}输出
如果运行上述程序，它将生成以下输出。
leaf nodes at end level are : 41 59 33 70
更新于：2019年8月22日
175 次浏览
广告