双极结型晶体管：定义、构造、类型

---

引言

双极结型晶体管是一种半导体器件。硅或锗是双极结型晶体管中使用的两种半导体材料。两个P-N结之间形成三层结构，分别称为发射极、基极和集电极。

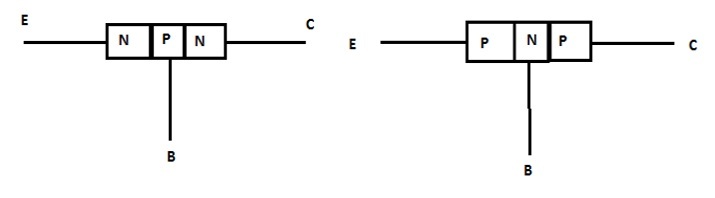
• 发射极层表示为E

• 集电极层表示为C

• 基极层表示为B

晶体管的中间部分称为基极层（B）。基极层是一层薄层，厚度约为25微米。晶体管的左侧层是发射极层（E），右侧层是集电极层（C）。

双极结型晶体管

用于放大信号的器件，由三层半导体材料和两个P-N结组成，称为双极结型晶体管（BJT）。当施加外部电源时，晶体管即可进行放大。基极层是薄层。晶体管的左侧部分是发射极层（E），右侧部分是集电极层（C）。发射极层高度掺杂。

但发射极必须提供大多数载流子。基极层与发射极相反，因为它是轻微掺杂的。集电极层也是轻微掺杂的，以接收更多载流子。根据这些特性，我们应该知道集电极和发射极不能互换。

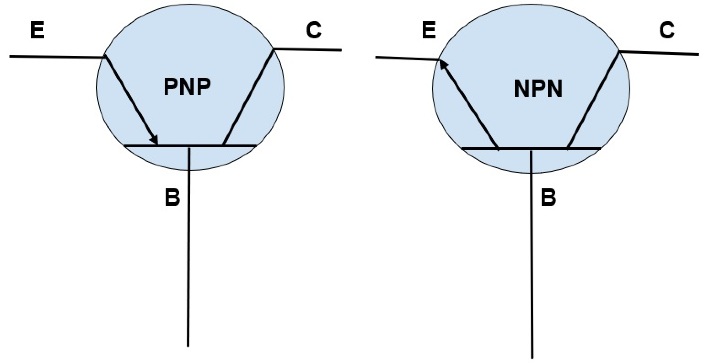
双极结型晶体管符号

箭头始终表示电流方向，在每个晶体管中从发射极区域到基极或从基极到发射极（从P到N）。它表示常规电流方向。在PNP晶体管中，箭头指向基极区域，表示发射极对基极和集电极是正的。在NPN晶体管中，箭头指向发射极区域，表示基极对发射极是正的。

双极结型晶体管构造

它由一块具有两个连续P-N结的独立半导体元件构成。硅或锗是双极结型晶体管中使用的两种半导体材料。我们已经知道晶体管由三层组成：发射极、基极和集电极。在PNP晶体管中，有两个PN结。左侧连接到发射极，中间部分是基极区域，右侧是集电极层。E-B和C-B交点是BJT的两个结。E-B结正向偏置，C-B结反向偏置。

双极结型晶体管的工作原理

BJT的工作区域包括饱和区、截止区和放大区。

饱和区

拐点的起点称为饱和区。饱和区位于原点和恒定点之间，在该点集电极电流变得恒定。

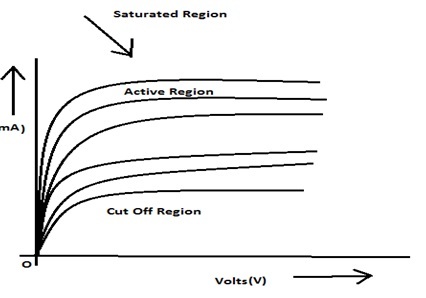
截止区

即使基极电流为零，晶体管中也存在非常低的集电极电流。基极电流为零的低区域称为截止区。

放大区

放大区位于曲线的中间，位于饱和区和截止区之间。放大区中的拐点是恒定的。在这个区域中，发射极-基极端子正向偏置，集电极-基极端子反向偏置。

双极结型晶体管的类型

• PNP BJT

• NPN BJT

PNP BJT

在PNP BJT中，N型材料的两侧都填充有P型半导体。

NPN BJT

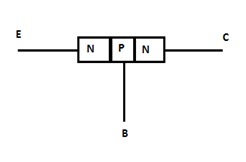
在NPN BJT中，左侧和右侧填充有N型半导体。P型半导体放置在这两种半导体之间。当电流进入发射极区域时，它将正号转换为负号。

双极结型晶体管的功能

PNP BJT和NPN BJT是两种类型的双极结型晶体管。PNP晶体管中存在背靠背的PN结。由于这两个结中存在的耗尽层，势垒增加了。电池提供外部电源。由于正向偏置，大量空穴通过端子进入基极。一些电子从基极进入发射极。这些电子与发射极中的空穴复合。当电子从发射极到基极的漂移增加时，发射极电流I_E增加。同样，也计算了基极电流和集电极电流。这就是双极结型晶体管的功能。

双极结型晶体管的电压、电荷控制和电流配置

C-E电流控制B-E电流。集电极-发射极电流给出电流-电压之间的关系。集电极电流中存在集中的次级载流子，因为它具有基极区域。

要操作双极结型晶体管，有三种类型的电路连接。

• 共基极（CB）模式

• 共发射极（CE）模式

• 共集电极（CC）模式。

BJT的应用

晶体管作为开关

通常BJT用作开关。例如，考虑NPN晶体管的共发射极配置。集电极与负载电阻和基极电阻串联连接。当输入为高电平时，晶体管饱和。当晶体管饱和时，电路中将流过最大电流。因此，晶体管处于导通状态。当输入为低电平时，基极-发射极结中没有电流流动。晶体管将处于关断状态。

晶体管放大器

放大是双极结型晶体管的主要功能。

结论

晶体管是一种用于增强信号的器件，由三层组成。具有两个P-N结的半导体材料称为双极结型晶体管（BJT）。它由三层组成：发射极、集电极和基极。BJT有两种类型：PNP BJT和NPN BJT。BJT的主要功能是计算三层的电流流动。BJT的应用包括用作开关、放大器、滤波器和振荡器。

常见问题

Q1. 什么是晶体管偏置？

A1. 当信号通过电路时，应保持发射极电压，并选择合适的运行点。这个过程称为晶体管偏置。

Q2. 什么是输出阻抗？

A2. 在恒定基极电流比下，放大区中C-E电压变化与集电极电流变化的比值称为输出阻抗。

$$\mathrm{输出阻抗,\:r_0=(\frac{\Delta V_{CE}}{\Delta I_C})I_B}$$

Q3. 晶体管的三个特性是什么？

A3.

• 输入特性

• 输出特性

• 转移特性

Q4. 请说明晶体管可以工作的偏置条件。

A3.

• 发射极-基极端子正向偏置，以便大量载流子从发射极推回，并且结提供少量电阻。

• 集电极-基极端子反向偏置，以便它接受大量载流子，并且结对电流提供大量电阻。

Q5. 定义电流增益β

A5. 在恒定的集电极-发射极电压下，集电极电流变化与基极电流变化的比值称为电流增益。

$$\mathrm{电流增益\:β=(\frac{\Delta I_C}{\Delta I_B})_{V_{CE}}}$$