数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学穆勒法C语言程序
给定一个浮点数x上的函数f(x)，我们可以有三个初始猜测来求函数的根。任务是找到函数的根，其中f(x)可以是任何代数或超越函数。
什么是穆勒法？
穆勒法由David E. Muller于1956年首次提出。穆勒法是一种求根算法，它从三个初始近似值开始寻找根，然后用二次多项式（抛物线）连接它们，然后使用二次公式来寻找二次方程的根作为下一个近似值。也就是说，如果x0、x1和x2是初始近似值，则通过求解由x0、x1和x2得到的二次方程来获得x3。然后，选择x0、x1和x2中两个最接近x3的值进行下一次迭代。
学习穆勒法的益处？
穆勒法是像二分法、试位法、割线法等求根方法之一，具有以下优点：
- 穆勒法的收敛速度高于其他方法。穆勒法的收敛速度为1.84，而割线法和线性法的收敛速度为1.62，试位法和二分法的收敛速度为1。收敛速度是指每次迭代我们向根靠近的程度。因此，穆勒法更快。
- 虽然它比牛顿-拉夫森法慢（牛顿-拉夫森法的收敛速度为2），但在穆勒法中，每次迭代计算导数更好。因此，穆勒法是一种有效的方法。
穆勒法的原理：
- 让我们假设三个不同的初始根x0、x1和x2。
- 现在，通过点x0、x1和x2的函数f(x)的值绘制抛物线。
抛物线p(x)的方程为：
p(x) = c + b(x – x2) + a(x – x2)²；其中a、b和c是常数。
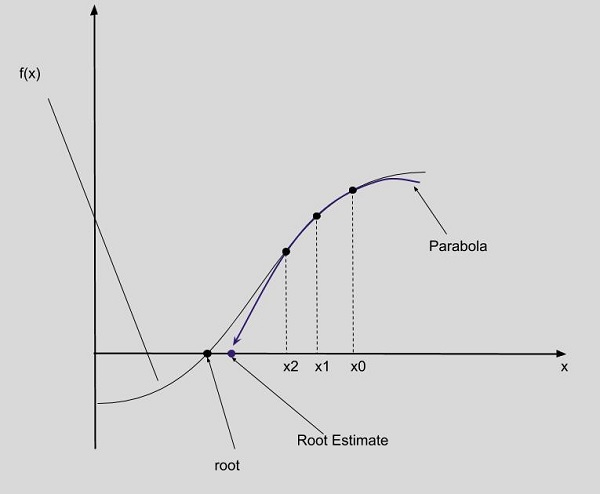
- 现在，找到抛物线与x轴的交点，例如x3。
- 如何找到抛物线与x轴的交点，即x3：
找到p(x)的根x3，其中p(x) = c + b(x – x2) + a(x – x2)²，使得p(x3) = c + b(x3 – x2) + a(x3 – x2)² = 0，对p(x)应用二次公式。由于我们必须取两个根中更接近x2的那个，我们将使用以下方程：
$$X_{3}-X_{2} = \frac{-2c}{b\pm\sqrt{b^{2}-4ac}}$$现在，由于p(x)应该更接近x2，所以我们将取上述方程中分母较大的值。
为了找到上述方程中的a、b和c，将x在p(x)中分别设为x0、x1、x2，并将这些值设为p(x0)、p(x1)和p(x2)，结果如下：
p(x0) = c + b(x0 – x2) + a(x0 – x2)² = f(x0) p(x1) = c + b(x1 – x2) + a(x1 – x2)² = f(x1) p(x2) = c + b(x2 – x2) + a(x2 – x2)² = c = f(x2)
因此，我们有三个方程来求解三个变量a、b和c。
现在，代入x3-x2的表达式，得到p(x)的根x3。
- 如果x3非常接近x2，则x3成为f(x)的根，否则重复查找下一个x3的过程，从之前的x1、x2、x3作为新的x0、x1、x2。
示例
Input: a = 1, b = 3, c = 2 Output: The root is 1.368809 Input: a = 1, b = 5, c = 3 Output: The root is 3.000001
算法
Start Step 1-> Declare and initialize a const MAX = 10000; Step 2-> In Function float f(float x) Return 1*pow(x, 3) + 2*x*x + 10*x – 20 Step 3-> In function int muller(float a, float b, float c) Declare i,result Loop For i = 0 and ++i Initialize f1 = result returned from calling function f(a) Initialize f2 = result returned from calling function f(b) Initialize f3 = result returned from calling function f(c) Set d1 = f1 - f3 Set d2 = f2 - f3 Set h1 = a - c Set h2 = b - c Set a0 = f3 Set a1 = (((d2*pow(h1, 2)) - (d1*pow(h2, 2))) / ((h1*h2) * (h1-h2))) Set a2 = (((d1*h2) - (d2*h1))/((h1*h2) * (h1-h2))) Set x = ((-2*a0) / (a1 + abs(sqrt(a1*a1-4*a0*a2)))) Set y = ((-2*a0) / (a1-abs(sqrt(a1*a1-4*a0*a2)))) If x >= y result = x + c Else result = y + c End if Set m = result*100 Set n = c*100 Set m = floor(m) and n = floor(n) If m == n Break End If Set a = b and b = c and c = result If i > MAX Print “Root can't be found using Muller method” Break End If End for If i <= MAX Print result Step 4-> In function int main() Declare and initialize the inputs a = 1, b = 3, c = 2 Call the function muller(a, b, c) Stop
示例
#include <stdio.h>
#include <math.h>
const int MAX = 10000;
//this function to find f(n)
float f(float x) {
// f(x) = x ^ 3 + 2x ^ 2 + 10x - 20
return 1*pow(x, 3) + 2*x*x + 10*x - 20;
}
int muller(float a, float b, float c) {
int i;
float result;
for (i = 0;;++i) {
// Calculating various constants required
// to calculate x3
float f1 = f(a);
float f2 = f(b);
float f3 = f(c);
float d1 = f1 - f3;
float d2 = f2 - f3;
float h1 = a - c;
float h2 = b - c;
float a0 = f3;
float a1 = (((d2*pow(h1, 2)) - (d1*pow(h2, 2))) / ((h1*h2) * (h1-h2)));
float a2 = (((d1*h2) - (d2*h1))/((h1*h2) * (h1-h2)));
float x = ((-2*a0) / (a1 + abs(sqrt(a1*a1-4*a0*a2))));
float y = ((-2*a0) / (a1-abs(sqrt(a1*a1-4*a0*a2))));
// Taking the root which is closer to x2
if (x >= y)
result = x + c;
else
result = y + c;
// checking for resemblance of x3 with x2 till
// two decimal places
float m = result*100;
float n = c*100;
m = floor(m);
n = floor(n);
if (m == n)
break;
a = b;
b = c;
c = result;
if (i > MAX) {
printf("Root can't be found using Muller method
");
break;
}
}
if (i <= MAX)
printf("The root is %f", result);
return 0;
}
// main function
int main() {
float a = 1, b = 3, c = 2;
muller(a, b, c);
return 0;
}输出
The root is 1.368809
926 次浏览
