数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究C++ 二分法程序
给定函数 f(x)，以及数字 a 和 b，其中 f(a) * f(b) > 0，并且函数 f(x) 应该位于 a 和 b 之间，即 f(x) = [a, b]。任务是使用二分法找到函数 f(x) 在区间 a 和 b 之间存在的根的值。
什么是二分法？
二分法用于在给定由 'a' 和 'b' 定义的限制范围内找到函数 f(x) 中根的值。函数的根可以定义为使得 f(a) = 0 的值 a。
示例
Quadratic equation F(x) = - 8 This equation is equals to 0 when the value of x will be 2 i.e. - 8 = 0 So, root of this quadratic function F(x) will be 2.
现在，如果函数 f(x) 在给定区间 [a..b] 内连续，并且 f(a) 的符号 ≠ f(b) 的符号，那么将存在一个属于区间 a 和 b 的值 m，使得 f(m) = 0
值 m [a..b] 使得 f(m) = 0
即 m 是根的值，它可能是多个
下图显示了区间 f(a) 和 f(b)。为了找到这些区间之间的根，将限制划分为多个部分并存储在变量 m 中，即：
m = (a + b) / 2
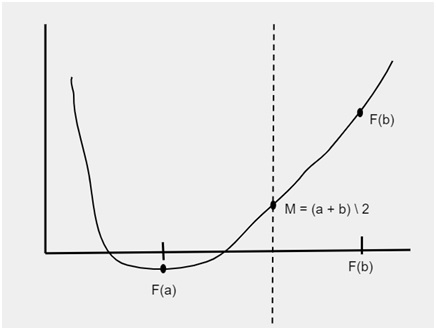
在限制划分后，将生成新的区间，如下面的图所示
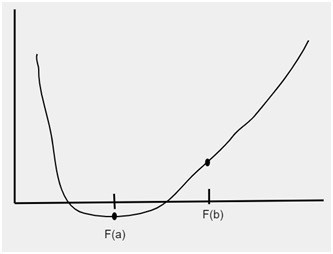
示例
Input-: x^3 - x^2 + 2 ; a =-500 and b = 100 Output-: The value of root is : -0.991821 Input-: x^3 - x^2 + 2 ; a =-200 and b = 300 Output-: The value of root is : -1.0025
我们在下面程序中使用的方案如下：
- 输入方程以及区间 a 和 b 的值
- 将区间划分为：m = (a + b) / 2
- 打印 m 是根
- 如果 f(m) ≠ 0
- 检查 f(a) * f(m) < 0
- 则根将位于 a 和 m 之间
- 检查 f(b) * f(m) < 0
- 则根将位于 b 和 m 之间
算法
Start Step 1-> In function double solution(double x) Return x*x*x - x*x + 2 Step 2-> In function bisection(double a, double b) If solution(a) * solution(b) >= 0 then, Print "You have not assumed right a and b " Return End If Set c = a Loop While (b-a) >= EP Set c = (a+b)/2 If solution(c) == 0.0 Break End If Else if solution(c)*solution(a) < 0 Set b = c End Else If Else Set a = c End Else End Print "The value of root” Step 3-> In function int main() Declare and Initialize inputs a =-500, b = 100 Call function bisection(a, b) Stop
示例
#include <iostream>
using namespace std;
#define EP 0.01
// An example function whose solution is determined using
// Bisection Method. The function is x^3 - x^2 + 2
double solution(double x) {
return x*x*x - x*x + 2;
}
// Prints root of solution(x) with error in EPSILON
void bisection(double a, double b) {
if (solution(a) * solution(b) >= 0) {
cout << "You have not assumed right a and b\n";
return;
}
double c = a;
while ((b-a) >= EP) {
// Find middle point
c = (a+b)/2;
// Check if middle point is root
if (solution(c) == 0.0)
break;
// Decide the side to repeat the steps
else if (solution(c)*solution(a) < 0)
b = c;
else
a = c;
}
cout << "The value of root is : " << c;
}
// main function
int main() {
double a =-500, b = 100;
bisection(a, b);
return 0;
}输出
The value of root is : -0.991821
更新于: 2019-12-20
15K+ 浏览量
广告