数据结构
网络
关系数据库管理系统(RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究(c) 解析输入字符串 id + id * id。
解答
步骤1 - 构造增广文法
(0) E′ → S
(1) E → E + E
(2) E → E ∗ E
(3) E → (E)
(4) E → id
步骤2 - 查找闭包和 goto 函数以构造 LR(0) 项目。
Closure(E′ → ∙ E) =
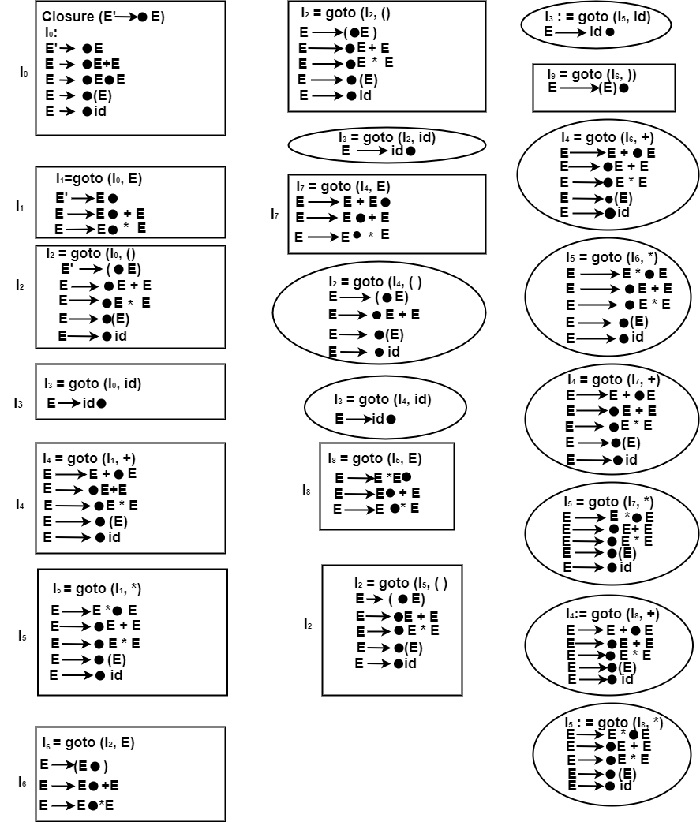
在 I9 上应用 goto
∵ 在 I9 上无法应用 goto，因为 E → (E). 中的点位于最后一个位置。
步骤3 - FOLLOW 的计算
应用规则 (1) FOLLOW
FOLLOW(B) = {$} (1)
- E → E + E
将 E → E + E 与 A → αBβ 比较
∴ α = ε，B = E，β = +E
∵ FIRST(β) = FIRST(+E) = {+}
∴ FOLLOW 的规则 (2a)
FOLLOW(E) = {+} (2)
应用规则 (3)
将 E → E + E 与 A → αB 比较
∴ A = E，α = E+，B = E
FOLLOW(E) = {FOLLOW(E)} (3)
- E → E ∗ E
应用 FOLLOW 的规则 (2) 和规则 (3)，我们得到
FOLLOW(E) = {*} (4)
FOLLOW(E) = {FOLLOW(E)} (5)
- E → (E)
应用规则 (2)
将 E → (E) 与 A → αBβ 比较
∴ FOLLOW(E) = {)} (6)
规则 (3) 无法应用于此产生式
因为 E → (E) 无法与 A → αB 比较
- E → id
FOLLOW 的规则 (2) 和 (3) 无法应用于 E → id。因为 E → id 无法与 A → αBβ 和 A → αB 比较。
组合 (1) 到 (6)，我们得到
FOLLOW(E) = {$, +, *, )}
步骤4 - 构造 SLR 解析表
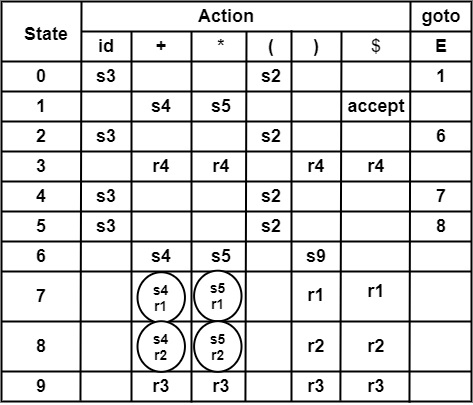
在解析表中，冲突发生在第 7 行、第 8 行和列 *、+。
在 Action[7, +]， Action[7, *]
Action[8, +]， Action[8, *] 出现移进-归约冲突。
结合性和优先级规则可以消除此冲突。
解析字符串 id + id * id
| 栈 | 输入 | 动作 |
|---|---|---|
| 0 | id + id * id $ | 移进 |
| 0 id 3 | + id * id $ | 根据 E → id 归约 |
| 0 E 1 | +id * id $ | 移进 |
| 0 E 1 + 4 | id * id $ | 移进 |
| 0 E 1 + 4 id 3 | * id $ | 根据 E → id 归约 |
| 0 E 1 + 4 E 7 | * id $ | 冲突，即 s5 或 r1 ∴ * 的优先级高于 + ∴ Action[7,*] = s5 所以，移进-归约，即 s5 |
| 0 E 1 + 4 E 7 * 5 | $ | 移进 |
| 0 E 1 + 4 E 7 * 5 id 3 | $ | 根据 E → id 归约 |
| 0 E 1 + 4 E 7 * 5 E 8 | $ | 根据 E → E * E 归约 |
| 0 E 1 + 4 E 7 | $ | 根据 E → E + E 归约 |
| 0 E 1 | $ | 接受 |
上述解析解决了 Action[7, *] 中的冲突问题。
所以，Action[7, *] = s5 而不是 r1。
类似地，解析字符串 id + id + id。
| 栈 | 输入 | 动作 |
|---|---|---|
| 0 | id + id + id $ | 移进 |
| 0 id 3 | + id + id $ | 根据 E → id 归约 |
| 0 E 1 | +id + id $ | 移进 |
| 0 E 1 + 4 | id + id $ | 移进 |
| 0 E 1 + 4 id 3 | +id $ | 根据 E → id 归约 |
| 0 E 1 + 4 E 7 | +id $ | 冲突，即 Action[7, +] = s4 或 r1。∴ + 是左结合的。0E1 + 4E7 将在移进 + 之前归约 ∴ Action[7, +] = r1 ∴ 根据 E → E + E 归约 |
| 0 E 1 | +id $ | 移进 |
| 0 E + 4 | id $ | 移进 |
| 0 E + 4 id 3 | $ | 根据 E → id 归约 |
| 0 E + 4 E 7 | $ | 根据 E → E + E 归约 |
| 0 E 1 | $ | 接受 |
因此，上述解析展示了如何解决 Action[7, +] 处的移进归约冲突
所以，Action[7, +] = r1 而不是 s4
类似地，其他条目，例如 Action[8, +] 和 Action[8, *] 可以通过采用字符串来解决。
id * id * id 和 id * id + id
解决方案是 Action[8, +] = r2 和
Action[8, *] = r2。
5K+ 次浏览
