考虑文法:
S → CC
C → c C | d
构建 LALR(1) 解析器的解析表。
解决方案
步骤1 − 构造 LR(1) 项目集。首先,应生成所有 LR(1) 项目集。
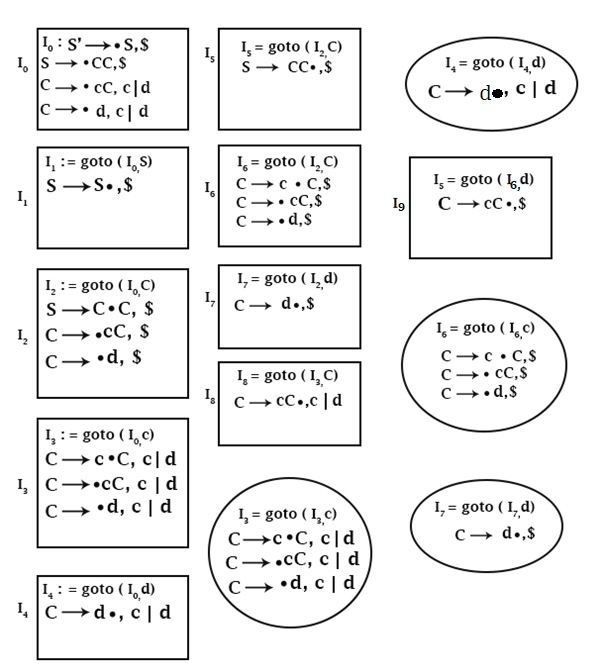
在这些状态中,状态 I3 和 I6 可以合并,因为它们具有相同的核心或第一部分,但展望符 (Look Ahead) 的第二部分不同。
同样,状态 I4 和 I7 是相同的。
同样,状态 I8 和 I9 是相同的。
因此,I3 和 I6 可以合并为 I36。
I4 和 I7 合并为 I47。
I8 和 I9 合并为 I89。
所以,状态将是

∴ I3 = goto(I0, c)
但 I3 , I6 合并为 I36
∴ I36 = goto(I0, c)
∴ I4 = goto(I0, d)
但 I4 , I7 合并为 I47
∴ I47 = goto(I0, d)
∴ I6 = goto(I2, c)
∴ I36 = goto(I2, c)
∴ I7 = goto(I2, d)
∴ I47 = goto(I2, d)
∴ goto(I3, C) = I8
但 I8 现在是 I89 的一部分
∴ goto(I36, C) = I89
同样,goto(I3, d) = I4, goto(I6, d) = I7 ∴ goto(I36, d) = I47
LALR 解析表构建
填充“移进”项 (s)
考虑 goto(I0, c) = I36
∴ Action[0, c] = s36
∴ 在状态 0 行和 c 列前面写入 s36。
同样,考虑
goto(I2, d) = I47
∴ Action[2, d] = 47
∴ 在状态 2 行和 d 列前面写入 s47。
填充“归约”项 (r)
考虑 A → α ∙ 形式的产生式,
例如,考虑状态
I47 = goto(I0, d)
C → d ∙, c |d |$
∴ C → d ∙, c |d |$ 具有 A → α ∙ 的形式。
由于 C → d 是给定问题中第 (3) 个产生式。
∴ 在状态 47 行和 c、d、$ 列前面写入 r3。
因为 c、d 是产生式 C → d ∙ , c | d 中的展望符。
填充 goto 项
这只对非终结符才能找到。
例如,考虑
goto(I0, S) = I1
∴ goto[0, S] = 1
填充“接受”项
由于 S′ → S ∙ , $ 在 I1 中
∴ 在状态 1 行和 $ 列前面写入 accept。
LALR 解析表也可以通过合并 CLR 解析的组合状态的行来获得,即合并对应于 3、6 的行,然后是 4、7,然后是 8、9。
生成的 LALR 解析表将是:
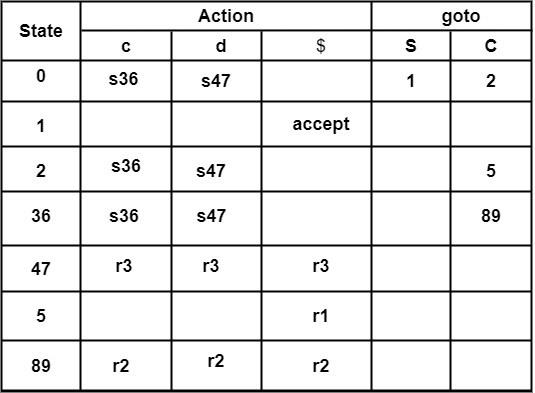


 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C语言编程
C语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP