在理论计算机科学（TOC）中解释操作符文法和优先级分析器

如果文法满足以下两个条件，则我们可以说这种类型的文法称为操作符优先级文法。

• 如果 ε 在其右部，则不存在任何产生式规则。

• 如果两个非终结符在其右部彼此相邻，则不存在任何产生式规则。

操作符文法具有以下属性：任何产生式的右部都不为空，也不包含两个相邻的非终结符。

示例

E-> E A E | id

A-> + | *

上述文法不是操作符文法，但我们可以将其转换为操作符文法，例如 -

E-> E + E | E * E | id

有三种优先级关系，如下所示 -

优先级表

优先级表

示例

输入字符串如下所示 -

id1 + id2 * id3

插入优先级关系后为 -

$ <· id1 ·> + <· id2 ·> * <· id3 ·> $

基本原理

• 从左到右扫描字符串，直到看到 ·> 并放置一个指针。

• 从右到左反向扫描字符串，直到看到 <·。

• 这两个关系 <· 和 ·> 之间的所有内容构成句柄。

• 用产生式的头部替换句柄。

操作符优先级分析算法

该算法如下所示 -

初始化：将 P 设置为指向输入字符串 w$ 的第一个符号。

重复 - 令 b 为栈顶符号，a 为 P 指向的输入符号。

如果 (a 为 $ 且 b 为 $)

返回

否则

如果 a ·> b 或 a =· b，则

将 a 推入栈

将 P 前进到下一个输入符号

否则如果 a <· b，则

重复

c -> 弹出栈

直到 (c .> 栈顶)

否则错误

结束

示例

使用该算法构建一个图。该图如下所示 -

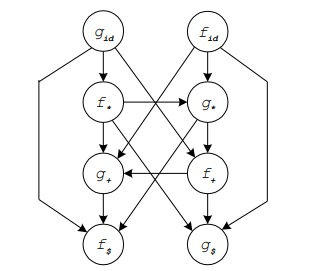
通过观察它，我们可以提取优先级函数，例如 -

Bhanu Priya

更新于： 2021年6月15日

2K+ 浏览量

开启您的 职业生涯

通过完成课程获得认证

开始学习