数据结构
网络
关系型数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究解释计算理论中语法的概念
在计算理论中，语法是一组生成句法正确的句子的形式规则的有限集合。
语法的正式定义是，它被定义为四个元组：
G=(V,T,P,S)
G 是一个语法，它包含一组产生式规则。它用于生成语言的字符串。
T 是终结符的最终集合。它用小写字母表示。
V 是非终结符的最终集合。它用大写字母表示。
P 是一组产生式规则，用于用字符串中的其他终结符（产生式的右侧）替换非终结符（产生式的左侧）。
S 是用于推导出字符串的起始符号。
语法由两个基本元素组成
终结符 - 终结符是使用语法生成的句子的组成部分，并使用小写字母（如 a、b、c 等）表示。
非终结符 - 非终结符参与句子的生成，但不是句子的组成部分。这些类型的符号也称为辅助符号和变量。它们用大写字母（如 A、B、C 等）表示。
示例 1
考虑一个语法
G = (V , T , P , S)
其中，
V = { S , A , B } ⇒ Non-Terminal symbols
T = { a , b } ⇒ Terminal symbols
Production rules P = { S → ABa , A → BB , B → ab , AA → b }
S = { S } ⇒ Start symbol示例 2
考虑一个语法
G=(V,T,P,S)
其中，
V= {S, A, B} ⇒ non terminal symbols
T = { 0,1} ⇒ terminal symbols
Production rules P = { S→A1B
A→0A| ε
B→0B| 1B| ε }
S= {S} ⇒ start symbol.语法的类型
不同类型的语法：
| 语法 | 语言 | 自动机 | 产生式规则 |
|---|---|---|---|
| 0 型 | 递归可枚举 | 图灵机 | 无限制 |
| 1 型 | 上下文相关 | 线性界限非确定性机器 | αAβ→αγβ |
| 2 型 | 上下文无关 | 非确定性下推自动机 | A→γ |
| 3 型 | 正则 | 有限状态自动机 | A→αB A→α |
表示语法类型在计算理论 (TOC) 中的图如下：
更新于: 2023-11-01
42K+ 次查看
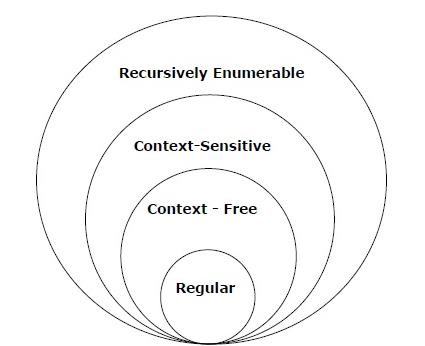
广告