如何在理论计算机科学（TOC）中将有限自动机（FA）转换为左线性文法？

如果一个文法的产生式右侧最多只有一个变量，则称为线性文法。

以下是一个线性文法的示例：

S→aSb/ε

在这里，如果你观察，我们可以通过划分……来写相同的产生式。

S→Ab

A→aAb

A→ε

左线性文法

如果一个文法的产生式右侧所有非终结符都位于最左侧，则称为左线性文法。

例如：

A→Sa/ε

转换步骤

将有限自动机（FA）转换为左线性文法的步骤如下：

步骤 1 - 取有限自动机的逆

步骤 2 - 写出右线性文法

步骤 3 - 然后取右线性文法的逆

步骤 4 - 最后，你将得到左线性文法

考虑如下所示的有限自动机：

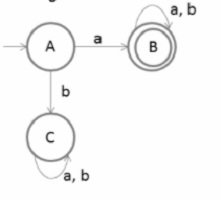
将最终状态作为初始状态，将初始状态作为最终状态，如下所示：

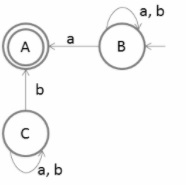
现在移除不可达状态，如下所示：

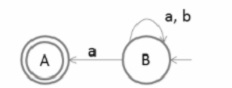
移除不可达状态后，状态转换图不是确定性有限自动机（DFA），因为状态 A 没有输出符号，而状态 B 在符号“a”上有两个输出。

因此，结果图看起来像非确定性有限自动机（NFA）。

首先，为最终状态转换图生成右线性文法：

      B→aA/aB/bB

      A→ε

现在反转右线性文法以生成左线性文法：

      B → Ba/Bb/Aa

      A→ε

更新于：2021年6月12日

4K+ 次浏览

开启你的职业生涯

通过完成课程获得认证

立即开始
广告