解释TOC中状态消除法的概念

将确定性有限自动机（DFA）转换为正则表达式（RE）有两种方法。这些方法如下：

  • Arden定理方法。
  • 状态消除法。

现在，让我们学习TOC中使用状态消除法。

状态消除法

步骤1

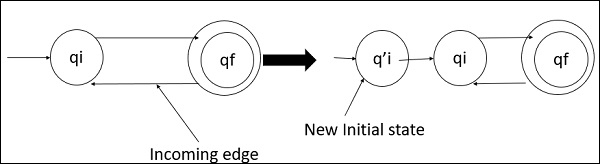
  • DFA的初始状态没有任何入边。
  • 如果初始状态存在任何入边，则需要创建一个新的初始状态，该状态没有入边。

入边和初始状态之间关系的示例如下：

步骤2

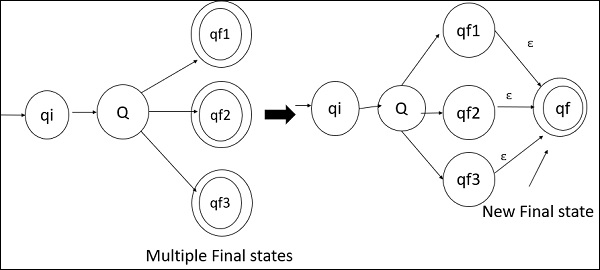
  • DFA中必须只有一个最终状态。
  • 如果DFA中存在多个最终状态，则需要将所有最终状态转换为非最终状态，并创建一个新的单个最终状态。

多个最终状态和最终状态的示例如下：

步骤3

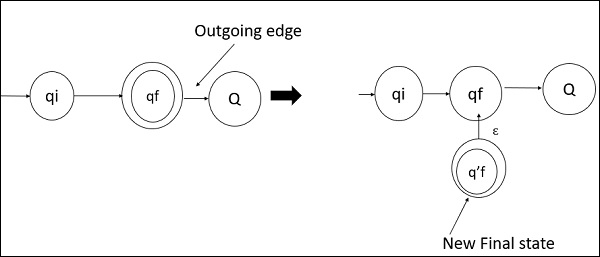
  • DFA的最终状态没有任何出边。
  • 如果最终状态存在任何出边，则需要创建一个新的最终状态，该状态没有任何出边。

出边和新最终状态的示例如下：

步骤4

  • 依次消除所有中间状态。这些状态可以按任何顺序消除。
  • 最后，将只剩下一个初始状态到最终状态的转换。
  • 此转换的成本就是所需的正则表达式。

更新于： 2021年6月11日

2K+ 浏览量

开启您的职业生涯

完成课程获得认证

开始学习
广告