使用 Arden 定理构造给定有限自动机的正则表达式

将确定性有限自动机 (DFA) 转换为正则表达式 (RE) 有两种方法。这些方法如下：

• Arden 定理方法。
• 状态消除方法。

让我们详细了解 Arden 定理方法。

Arden 定理

设 P 和 Q 为两个正则表达式。

如果 P 不包含空字符串，则关于 R 的以下方程，即 R = Q + RP，

其唯一解为 R = QP*

这里，

• 有限自动机 (FA) 没有 ε 移动。
• 它必须只有一个初始状态 q1。
• 其状态为 q1、q2、q3、…、qn。最终状态可以是某个 qi，其中 i<=n。
• qi 是表示有限自动机接受的字符串集的正则表达式，即使 qi 是最终状态。

现在让我们考虑一个问题，即如何使用 Arden 定理构造给定的有限自动机。

问题

通过应用 Arden 定理，找出给定有限自动机的正则表达式。

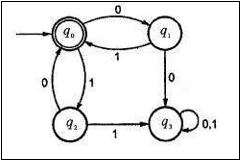
解决方案

让我们看看这些方程。

q₀ = q₁ + q₂₀+ E

q₁ =q₀0

q₂ =q₀1

q₃ = q₁0 + q₂1+ q₃(0+1)

让我们首先解决 q₀，如下所示：

q₀ = q₁ + q₂₀+ E

q₀ = q₁ + q₀10+ E

q₀ = q₀(01 +10)+ E

q₀ = E(01+10)*

q₀ = (01+10)*

·: R = Q+ RP

=> QP* 其中

R =q₀ ,Q =e, P= (01 + 10)

因此，正则表达式如下：

r = {01+10)*

由于 q0 是最终状态，我们只对 q0 感兴趣。

Bhanu Priya

更新于： 2021年6月11日

869 次查看

开启你的 职业生涯

通过完成课程获得认证

立即开始