数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学构建用于所有长度回文串的下推自动机
L = {ww’ | wcw’, w ∈ {0, 1}*}，其中 w’ 是 w 的逆序。
这是在字母表 {0,1} 上所有奇数和偶数长度回文串的语言。
为了构建所有长度的回文串，让我们使用非确定性下推自动机 (NPDA)。
为了构建 wcw’，我们需要检查字符串是否为奇数长度，如果到达中间元素 'c'，则处理它并移动到下一个状态，而无需对堆栈进行任何更改。
示例
给定的字符串是 1 1 0 0 1 1 1 1 0 0 1 1
结果 - 接受
给定的字符串是：1 0 1 0 1 0 1 0 1
结果 - 接受
状态转换图如下：
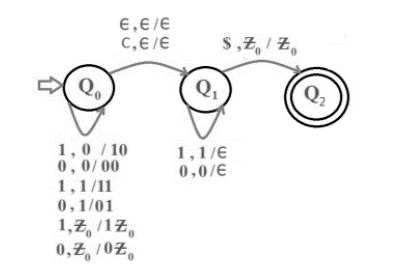
步骤 1 - 接收到 0 或 1 时，将元素压入堆栈顶部，并检查输入字符串是否为偶数长度，如果是，则检查它是否到达输入字符串的后半部分。
假设，如果输入字符串是奇数长度，则检查它是否到达中间元素。
步骤 2 - 如果输入字符串是偶数长度并且到达前半部分的最后一个元素，则将该元素压入堆栈顶部并进行 epsilon 移动到下一个状态；或者，如果输入字符串是奇数长度，则在接收到元素 'c' 时，移动到下一个状态，而无需对堆栈进行任何更改。
步骤 3 - 接收到一个元素时，检查扫描的符号：如果扫描的符号是 '0' 并且堆栈顶部也包含 '0'，或者扫描的符号是 '1' 并且堆栈顶部也包含 '1'，则从堆栈顶部弹出该元素；否则，移动到死状态。
重复步骤 3，直到字符串为空。
步骤 4 - 检查扫描的符号是否为 '$' 并且堆栈不包含任何元素，则移动到最终状态；否则，移动到死状态。
更新于：2021年6月15日
10K+ 次浏览
广告