数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学比较下推自动机和线性有界自动机
让我们了解计算理论 (TOC) 中的下推自动机 (PDA) 和线性有界自动机 (LBA)。
下推自动机
PDA 可以正式描述为七元组 (Q, Σ, S, δ, q0, I, F)
其中：
- Q 是有限数量的状态
- Σ 是输入字母表
- S 是栈符号
- Δ 是转移函数：QX(ΣU{e})XSXQ
- q0 是初始状态 (q0属于Q)
- I 是初始栈顶符号
- F 是接受状态集 (F属于Q)
下推自动机是一种有限状态机，它配备了一个作为下推存储器工作的存储设备。
下推自动机等价于上下文无关文法（也称为乔姆斯基2型文法），这意味着，给定一个上下文无关文法G，可以设计出一个下推自动机A来识别G生成的句子。
这种上下文无关文法和下推自动机之间的关系最早由乔姆斯基（1962年）描述。Yngve（1960年）早些时候使用与下推自动机密切相关的机器来模拟人类处理器分析由上下文无关文法生成的具有各种不同结构的句子所需的瞬时存储器。
他的方法的基本原理仍然应用于短期记忆和句子处理的研究，其中下推自动机的存储器用作瞬时存储器的模型，用于分析具有不同结构的句子。
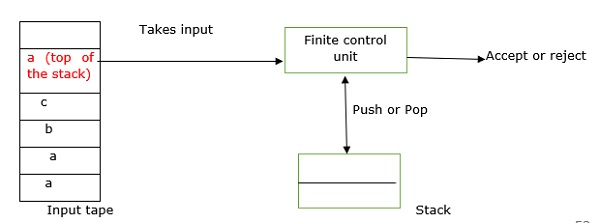
PDA 的组成部分
下推自动机由四个部分组成：
- 控制单元。
- 读取单元。
- 输入带。
- 存储单元。
控制单元、读取单元和带的操作与有限状态自动机相同，只是下推自动机的控制单元执行的转换涉及将符号存储到存储单元以及从存储单元检索符号的操作。
下推自动机的存储单元作为一个堆栈或下推存储器工作，这导致了这种抽象机的名称。
线性有界自动机
线性有界自动机 (LBA) 称为多轨图灵机，它只有一个与输入完全相同长度的磁带。这似乎相当合理。我们允许计算设备仅使用在其计算开始时给出的存储空间。
作为安全措施，我们将在我们的 LBA 磁带上使用结束标记，并且永远不允许机器越过它们。这将确保维护存储边界，并有助于防止我们的机器离开磁带。此时，接受集的问题就出现了。让我们像图灵机一样让线性有界自动机接受。
因此，对于 LBA 来说，停止意味着接受。对于这些新的机器，计算仅限于由常数（轨道数）乘以输入长度所界定的区域。这非常类似于一个编程环境，其中变量的值的大小是有界的。
2K+ 次浏览
