数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济
心理学
社会科学
时尚研究
法律研究理论计算机科学中的线性有界自动机是什么？
确定性线性有界自动机 (LBA) 是 9 元组自动机
G = ( Q, Σ, E, δ, ε, q0, GL, GR, F)
其中：
Q 是所有状态的集合
Σ 是所有终结符的集合
E 输入字母表。
δ 是转换的集合
q0 初始状态
GL 磁带左边界
GR 磁带右边界。
F 终态集合
线性有界自动机是一种具有有限长度的有界磁带的多轨非确定性图灵机。
长度 = 函数（初始输入字符串长度，常数 c）
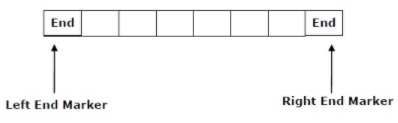
线性有界自动机中的计算限制在常数界定的区域内。此处的输入字母表包含两个特殊符号，用作左端标记和右端标记。这说明转换既不会移动到磁带的左端标记的左侧，也不会移动到磁带的右端标记的右侧。
确定性线性有界自动机是上下文相关的，且空语言的线性有界自动机是不可判定的。
问题
如何构造线性有界自动机来接受语言 L={an|n=m2,m>=1}？
解决方案
对于给定的语言 L={an|n=m2,m>=1}，它生成的字符串为 -
L(G) ={a.aa.ab.aaa.aab.abb…….}
S aA, A,aA,A,B,B,bB,B
S aA, aB, a, a (可接受)
S aA, aaA aaB, aa, aa (可接受)
S aA, aB abB, ab, ab (可接受)
SaA, aaA, aaaA, aaa aaa (可接受)
SaA, aaA, aaB, aabB aab, aab (可接受)
SaA, aB, abB, abbB, abb, abb (可接受)
在这里，我们可以根据产生式集证明 L(G) 中的每个字符串都是可接受的语言。
G={{S,AB};{a,b}S, {S aA, A,aA/B, B/bB}}。
更新于： 2021 年 6 月 14 日
9K+ 次观看
广告