数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究什么是理论计算机科学中的 Kleene 定理？
Kleene 定理指出以下三个陈述的等价性：
有限自动机接受的语言也可以被状态转换图接受。
状态转换图接受的语言也可以被正则表达式接受。
正则表达式接受的语言也可以被有限自动机接受。
Kleene 定理证明第一部分
有限自动机接受的语言也可以被状态转换图接受。
考虑一个例子，设 L=aba 在字母表 {a,b} 上。
Kleene 定理的第三部分
正则表达式接受的语言也可以被有限自动机接受。
定理
任何可以用正则表达式定义的语言都可以被某个有限状态机 (FSM) 接受，并且也是正则的。
证明
证明是通过构造来进行的。
对于给定的正则表达式 α，我们可以构造一个 FSM M，使得
L (α) = L (M)
如果 α 是任何 c ∈ Σ，我们可以构造一个简单的 FSM，如下所示：
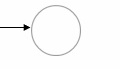
如果 α 是 φ，我们构造一个简单的 FSM，如下所示：
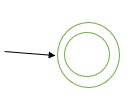
如果 α 是 €，我们构造一个简单的 FSM，如下所示：
让我们构造 FSM 来接受由正则表达式定义的语言，这些正则表达式利用连接、并集和 Kleene 星号运算。
步骤 1
设 β 和 γ 是在字母表 Σ 上定义语言的正则表达式。
如果 L(β) 是正则的，则它被某个 FSM 接受。
M1 = (Q1, Σ, δ1, q1, F1)
设 L(γ) 是正则的，则它被某个 FSM 接受。
M2= (Q2, Σ, δ2, q2, F2)
步骤 2
如果正则表达式 α= β ∪ γ，并且 L(β) 和 L(γ) 都是正则的，
那么我们构造 M3=( Q3, Σ, δ3, q3, F3)，使得
L(M3)=L(α)=L(β) ∪ L(γ)
步骤 3
设 P 接受 L = {a}，Q 接受 L = {b}，则 R 可以表示为 P 和 Q 的组合，使用提供的运算，如下所示：
R = P+ Q
相同的转换图如下所示：
我们在转换图中观察到以下内容：
在并集运算的情况下，我们可以有一个新的起始状态。从那里，一个空转换过程进入两个有限状态机的起始状态。
两个有限自动机的最终状态转换为中间状态。最终状态统一为一个，可以通过空转换遍历。
17K+ 次浏览
