数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学什么是TOC中的NP完全性？
**非确定性多项式(NP)问题**有点难以理解。就解决NP问题而言，运行时间不是多项式的。它可能是O(n!)或更大的级别。
但是，这类问题给定一个特定的解决方案，检查该解决方案的运行时间是多项式的。
例如，数独游戏。
NP难问题
如果一个用于解决NP难问题的算法可以转化为解决任何NP问题，则称该问题为NP难问题。那么我们可以说，这个问题至少与任何NP问题一样难，但它可能更难或更复杂。
NP完全问题
NP完全(NPC)问题是同时存在于NP和NP难类中的问题。也就是说，NP完全问题可以在多项式时间内验证，并且任何NP问题都可以在多项式时间内简化为该问题。
如果一个问题在NP类中并且与NP中任何问题一样难，则该问题属于NPC类。如果NP中的所有问题都可以在多项式时间内简化为它，即使它本身可能不在NP类中，则称该问题为NP难问题。
如果任何这类问题存在多项式时间算法，则NP中的所有问题都可以用多项式时间求解。这些问题称为NP完全问题。NP完全性对于理论和实践都具有重要意义。
NP完全性的定义
如果一个语言M满足以下两个条件，则它是NP完全的：
M属于NP。
NP中的每个A都可以多项式时间归约到M。
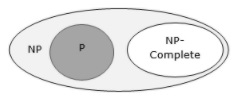
如果一个语言满足第二个性质，但不一定满足第一个性质，则该语言M被称为NP难。
非正式地，如果存在某个NP完全问题A可以图灵归约到M，则搜索问题M是NP难的。
NP完全问题
目前尚不知道存在多项式时间算法的NP完全问题的例子如下：
确定一个图是否具有哈密顿循环
确定布尔公式是否可满足等。
NP难问题
以下问题是NP难的
电路可满足性问题
集合覆盖问题
顶点覆盖问题
旅行商问题
更新于：2021年6月14日
13K+浏览量
广告