数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究证明顶点覆盖在理论计算机科学（TOC）中是NP完全的
它是图G的顶点子集（最小尺寸），使得G中的每条边都至少与G中一个顶点相关联。
顶点覆盖（VC）问题
为了证明VC是NP完全的，我们必须证明以下几点：
VC是非确定性多项式（NP）的。
一个NPC问题可以归约到VC。
为了证明VC是NP，找到一个验证器，它是一个顶点子集，它是VC，并且可以在多项式时间内进行验证。对于一个有n个顶点的图，它可以在O(n2)时间内得到证明。因此，VC是NP。
现在考虑“团”问题，它是NPC，并将它归约到VC以证明NPC。图G的团是顶点的子集，使得这些顶点在给定的图G中形成一个完全子图。
下面给出了VC问题的两个图标题（a）和（b）：
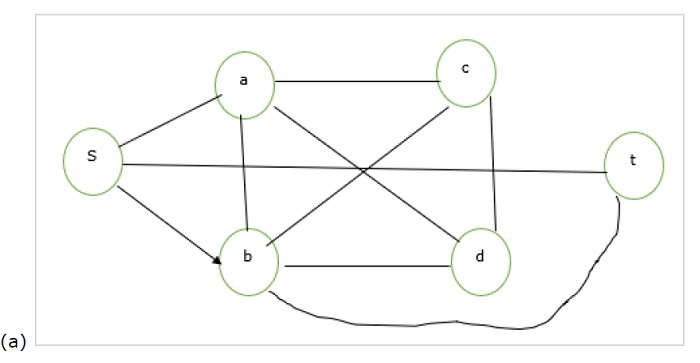
考虑图（a），这里团是{a,b,c,d}。
现在计算一个如图（b）所示的图，如下所示：
图（a）中所有顶点的完全图 - （a）
对于图（b），我们可以说顶点覆盖是{s,t}，它覆盖了（b）的所有边。这个{s,t} = {a,b,c,d,s,t} – {图（a）的团} 因此，反过来，我们可以说我们可以将团归约到VC问题，反过来也可以找到给定无向图的VC和团。这意味着VC是NP完全可归约的。
因此证明了VC是NPC。
更新于：2021年6月14日
7K+ 浏览量
广告