数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学证明哈密顿路径问题在理论计算机科学（TOC）中是NP完全的
哈密顿环是一个沿着图G的n条边的环路路径，它访问每个顶点一次并返回到其起始顶点。
示例
下面是一个哈密顿环路路径的示例：
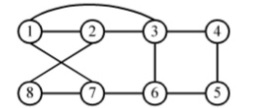
哈密顿环路路径：1,2,8,7,6,5,4,3,1
旅行商问题是NP完全的
旅行商问题(TSP)有一个销售员和一组城市。销售员需要从某个城市出发，访问每个城市一次，然后返回到同一个城市，即回到起始位置。这个问题的挑战在于，旅行商希望最小化总行程长度。
证明
为了证明TSP是NP完全的，首先尝试证明TSP属于非确定性多项式(NP)类。
在TSP中，我们必须找到一个巡回路线，并检查该巡回路线是否包含每个顶点一次。
然后，我们计算巡回路线的边的总成本。最后，我们检查成本是否最小。这可以在多项式时间内完成。
因此，TSP属于NP类。
接下来，我们必须证明TSP是NP难的。
为了证明这一点，一种方法是证明哈密顿圈问题 ≤p TSP（因为我们知道哈密顿圈问题是NP完全的）。
假设G = (V, E)是哈密顿圈问题的一个实例。
因此，构造了一个TSP实例。我们可以创建一个完全图G' = (V, E')，其中
E′={(i,j):i,j∈Vandi≠j
Thus, the cost function is defined as follows:
t(i,j)= 0 if (i,j) ∈ E
=1 otherwise现在，假设在G中存在哈密顿圈H。G'中H的每条边的成本为0，因为每条边都属于E。因此，H在G'中的成本为0。因此，如果图G具有哈密顿圈，则图G'具有成本为0的巡回路线。
现在让我们假设G'具有成本最多为0的巡回路线H'。根据定义，E'中边的成本为0和1。因此，由于H'的成本为0，每条边的成本必须为0。我们最终得出结论，H'只包含E中的边。
最终证明了：当且仅当G'具有成本最多为0的巡回路线时，G才具有哈密顿圈。因此，TSP是NP完全的。
更新于：2021年6月14日
5K+ 次浏览
广告