数据结构
网络
关系数据库管理系统(RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学图的支配集是NP完全问题的证明
图的支配集是NP完全问题，指的是顶点的子集，使得子集中的每个顶点或其相邻顶点都在子集中。NP的完整形式是“非确定性多项式”，它将在多项式时间内检查问题，这意味着我们可以在多项式时间内检查解是否正确。多项式时间对代码具有最佳复杂度，例如线性搜索的时间复杂度为– n, 二分查找为– logn，归并排序为– n(log)n等。NP完全图在合理的时间内提供了一个很好的解决方案。此应用用于网络控制、计算机实验室拓扑创建、社交网络和分布式计算领域。
让我们了解并检查节点是否在NP完全问题中具有图的支配集。
一个顶点被认为支配自身及其每个邻居。
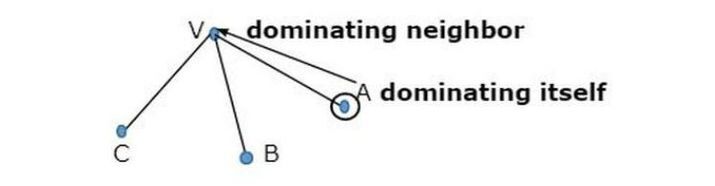
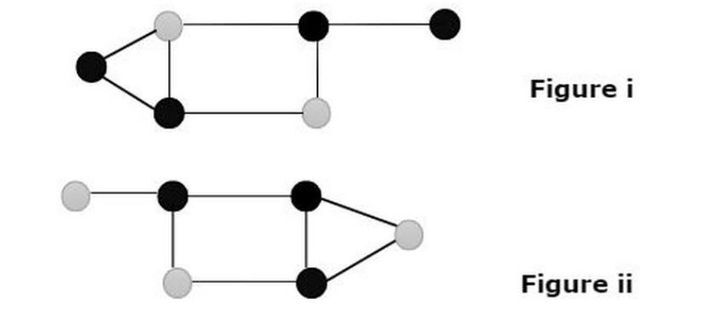
我们看到有两幅图显示图中灰色节点的支配性质。
G = V, E
参数
G被认为是一个图，V被认为是一个顶点，E被认为是一条边。
给定一个图G(V, E)和一个整数k，确定一个图是否具有大小为k的支配集。为问题指定的一个输入被认为是问题的实例。图G (V, E)和整数k是支配集问题的例子，它询问图G中是否可以有一个支配集。由于NP完全问题根据定义既属于NP又属于NP-hard，因此证明一个问题是NP完全的问题有两个组成部分：
支配集在NP完全问题中
如果存在一个NP问题Y可在多项式时间内归约到X，则X是NP完全的。NP完全问题与NP问题一样困难。如果一个问题同时属于NP和NP-Hard问题，则它是NP完全的。在一个非确定性图灵机中，可以在多项式时间内解决NP完全问题。当一个问题是np完全问题时，它同时具有np和np hard的特性。
这意味着具有np解的问题可以在多项式时间内验证。
NP完全问题具有支配集的真实例子，例如：
决策问题。
一致的图。
非确定性搜索算法
NP_search( key ) {
arraylist[100];
i = array_check(key);
if(list[i]==key) {
searching found at index i.
} else {
searching found at index i.
}
}
因此，该算法的总时间复杂度为O(1)，但我们不知道哪种搜索技术更适合解决这个问题，这被称为非确定性算法。
支配集在NP-hard问题中
如果存在一个NP完全问题Y可在多项式时间内归约到X，则问题X是NP-Hard的。NP-Hard问题与NP完全问题一样困难。NP-Hard问题不必属于NP类。
如果每个NP问题都可以在多项式时间内解决，则它被称为NP-Hard。很多时候，一个特定的问题被用来解决和简化其他问题。
NP-hard问题具有支配集的真实例子，例如：
哈密顿回路
优化问题
最短路径
结论
我们学习了图的支配集是NP完全的概念。我们看到了离散数学是如何作为一个重要方面来连接这些问题的，例如哈密顿回路、最短路径等。在编程方面，NP完全问题是一类难以找到但易于在多项式时间内验证解的问题。
396 次浏览
