什么是 TOC 中的判定问题？

判定问题 Q 是一个问题的集合，每个问题都有一个 Yes 或 No 的答案。比如，“10 是一个完全平方数吗？”。这是一个判定问题的例子。判定问题通常包含的都是一组无限关联的问题。

示例

问题 PSQ 用于确定一个任意自然数是不是完全平方数，它有一些像下面这样的值得怀疑的问题：

  • q0: 0 是完全平方数吗？
  • q1: 1 是完全平方数吗？
  • q2: 2 是完全平方数吗？

解决方法

判定问题 Q 的解决方法是一个算法，它可以确定每个问题 q ϵ Q 的近似答案。

解决判定问题的算法必须是：

  • 完全的。
  • 机械的。
  • 确定的。

满足上述所有属性的程序通常被称为有效的。

如果一个问题可以表示为一组从递归语言中接受的字符串，那么该问题就被称为可判定问题。

因为确定性多轨多磁带机计算可以在标准的图灵机上模拟，所以使用这些机器的解法也可以确定问题的可判定性。

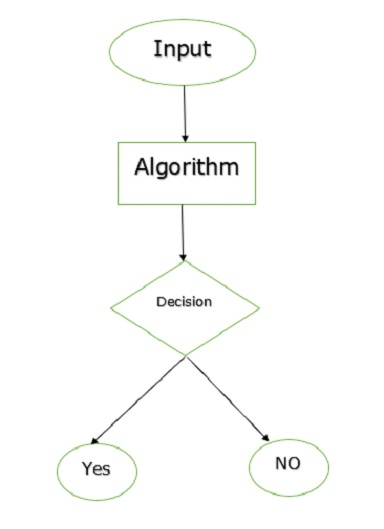
判定问题如下：

上次更新： 2021 年 6 月 12 日

2K+ 次浏览

开启 职业生涯

完成课程认证

开始学习
广告