TOC 中的归纳假设是什么？

归纳法是数学中一个强大的工具。它是一种证明对所有自然数都成立的命题的方法。

假设 - 正式证明可以使用演绎证明和归纳证明。演绎证明由一系列语句组成，这些语句以逻辑推理的方式给出，以证明第一个或初始语句。初始语句称为假设。

假设存在一个 k > 0，使得对于任何正则表达式 r，其中 0 < OP(r) < k，存在一个 NFA-s 使得 L(M) = L(r)。此外，假设 M 只有一个最终状态。

归纳步骤

令 r 为一个具有 k + 1 个运算符（OP(r) = k + 1）的正则表达式，其中 k + 1 >= 1。

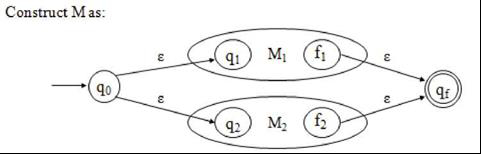
情况 1 - r = ri + r2

由于 OP(r) = k +1，因此 0<= OP(n)，OP(r2) <= k。根据归纳假设，存在非确定性有限自动机 (NFA-s) 机器 M1 和 M2，使得 L(Mt) = L(n) 和 L(M) = L(r2)。

此外，M1 和 M2 都只有一个最终状态。我们可以构建如下所示的 M -

情况 2 - r = r1r2

由于 OP(r) = k+1，因此 0<= OP(r1)，OP(r2) <= k。根据归纳假设，存在 NFA-s 机器 M1 和 M2，使得 L(M1) = L(n) 和 L(M2) = L(r2)。

此外，M1 和 M2 都只有一个最终状态。我们现在可以构建如下所示的 M -

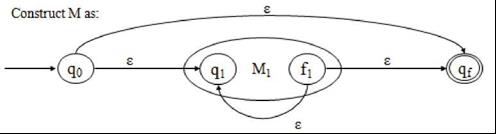
情况 3 - r = ri*

由于 OP(r) = k+1，因此 0<= OP(ri) <= k。根据归纳假设，存在一个 NFA-s 机器 M1，使得 L(M1) = L(n)。

此外，M1 只有一个最终状态。因此，我们可以如下构建 M -

Bhanu Priya

更新于: 2021年6月12日

2K+ 次查看

开启你的 职业生涯

通过完成课程获得认证

开始学习