什么是计算理论 (TOC) 中的可判定性？

在计算理论 (TOC) 中，有两种类型的语言：

• 可判定语言

• 不可判定语言

如果一个问题存在解，并且可以构造相应的算法，则称该问题为可判定问题。

可判定问题的例子

找出1到50之间所有奇数。

对于这个问题，我们可以很容易地通过构造算法找到解决方案。就图灵机 (TM) 而言，如果一个问题是可判定的，那么图灵机无论是否接受其输入都会停机。

就有限自动机 (FA) 而言，“可判定”指的是测试确定性有限自动机 (DFA) 是否接受输入字符串的问题。可判定语言对应于算法可解的判定问题。

可判定性定理

在 Σ 上的语言 L 被称为可判定的，如果：

• 存在一个接受语言 L 的图灵机 M

• 对于所有 w ∈ Σ*，M 都会停机

可判定性

对于递归语言

• 如果存在一个图灵机能够接受 L 中的所有字符串并拒绝 L 之外的所有字符串，则称语言“L”为递归语言。

• 图灵机每次都会停机，并为每一个输入给出接受或拒绝的答案。

递归可枚举语言：

• 如果存在一个图灵机能够接受 L 中的所有输入并停机，则称语言“L”为递归可枚举语言。

• 但对于不在 L 中的输入，可能停机也可能不停机。

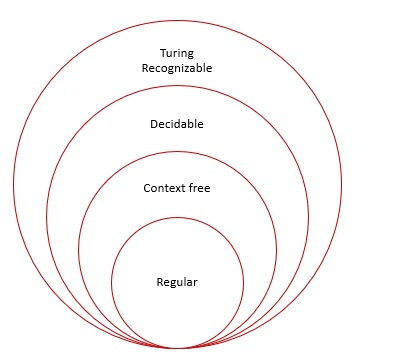
如果语言‘L’是递归语言，则它是可判定的。

所有可判定语言都是递归语言，反之亦然。

下图解释了可判定语言：

Bhanu Priya

更新于：2021年6月14日

浏览量 10K+

启动您的职业生涯

完成课程获得认证

开始学习