在理论计算机科学(TOC)中解释非确定性有限自动机。
NFA 代表非确定性有限自动机。与给定正则语言的 DFA 相比,构建 NFA 比较容易。
当存在许多从当前状态到下一个状态的特定输入路径时,有限自动机被称为 NFA。
每个 NFA 都可以转换为 DFA,但每个 NFA 都是非 DFA。
NFA 的定义方式与 DFA 相同,但以下两个例外情况除外:
- 它包含多个下一个状态。
- 它包含 ε 转移。
示例
状态转换图如下所示:
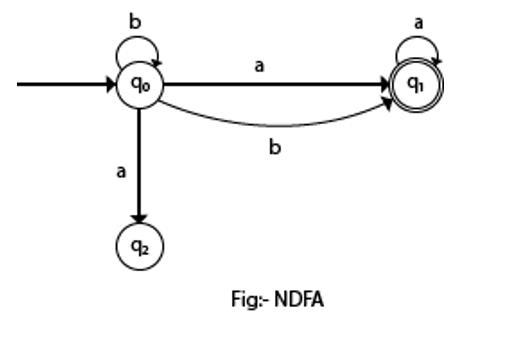
在上面的 NFA 中,很明显,存在许多从当前状态到下一个状态的特定输入路径。(状态 q0 在输入“b”时,它会进入 q0 本身和 q1)。
非确定性有限自动机也具有与 DFA 相同的五个状态,但具有不同的转换函数,如下所示:
δ: Q X Σ -> 2Q
非确定性有限自动机定义为一个 5 元组,
M=(Q, Σ, δ,q0,F)
其中,
- Q:状态的有限集合
- Σ:输入符号的有限集合
- q0:初始状态
- F:最终状态
- δ:转移函数:Q X Σ -> 2Q
NFA 的图形表示
NFA 可以用称为状态图的有向图来表示。
在图形化表示 NFA 时,需要考虑以下因素:
- 状态由顶点表示。
- 用输入字符标记的弧表示转换。
- 初始状态用箭头标记。
- 最终状态用双圆圈表示。
示例 1
Q = {q0, q1, q2}
Σ = {0, 1}
q0 = {q0}
F = {q2}
状态转换图
状态转换图如下所示:

状态转换表
状态转换表如下所示:
| 当前状态 | 输入 0 的下一个状态 | 输入 1 的下一个状态 |
|---|---|---|
| ->q0 | q0,q1 | q1 |
| q1 | q2 | q0 |
| *q2 | q2 | q1,q2 |
解释
- 步骤 1 - q1 是初始状态,在输入“0”时,它会进入多个状态 q0 和 q1,在输入“1”时,会进入状态 q1。
- 步骤 2 - q1 是中间状态,在输入“0”时,会进入状态 q2,这是一个最终状态,在输入“1”时,会进入状态 q0。
- 步骤 3 - q2 是最终状态,在输入“0”时,它会进入 q2 本身,在输入“1”时,它会进入多个状态 q1 和 q2。

广告

 数据结构
数据结构 网络
网络 关系数据库管理系统
关系数据库管理系统 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 编程
C 编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP