数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究什么是非确定有限自动机 (NFA)？
非确定性意味着从某个状态出发，在相同的输入符号上可能存在多个可能的转移。对于给定的输入，输出是非确定的。NFA 可以表示为非确定有限状态机。
NFA 可以用 5 元组 (Q,$\sum$,$\delta$,q0,F) 表示。
Q 是一个有限的非空状态集。
$\sum$ 是一个有限的输入符号集。
$\delta$ 是从当前状态转移到下一个状态的转移函数。
∴ $\delta$:Q x $\sum$ → 2Q
q0 ∈ Q 是初始状态。
F \subseteq Q 是终结状态集。
示例 1 - 为正则表达式 a(a+b)*ab 绘制 NFA
解决方案
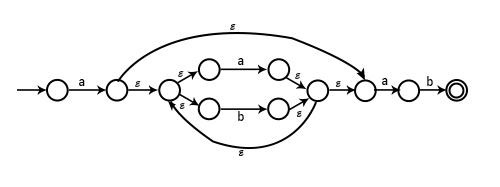
示例 2 - 为 a + b + ab 绘制 NFA
解决方案
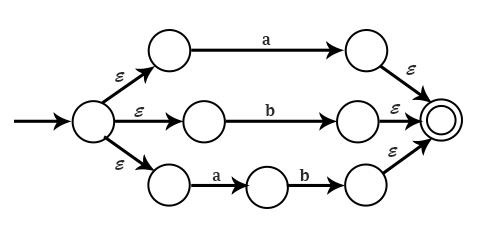
示例 3 - 令 M=(Q,∑,$\delta$,q0,F) 为一个 NFA。证明对于任何 qϵQ 和 a ϵ Σ,$\delta$′(q,a)= $\delta$(q,a)
解决方案
令 M=(Q,∑,$\delta$,q0,F) 为识别语言 L 的 NFA。则满足以下条件的 DFA，M′=(Q1,∑,$\delta$′,q′0,F′) 识别 L：Q1=2Q，即 Q 的所有子集的集合。
q′0={q0}
$\delta$(q,a)=∪pϵq$\delta$(p,a) 对于 Q1 中的每个状态 q 和 Σ 中的每个符号 a 以及
F={qϵQ1|q∩F2≠ф}
为了获得 DFA M′=(Q1,Σ,$\delta$′,q′0,F′)，它接受与给定 NFA，M=(Q,∑,$\delta$,q0,F) 相同的语言。可以按如下步骤进行 -
步骤 1 - 最初 Q1=ф
步骤 2 - 将 {q0} 放入 Q1 中。{q0} 是 DFA M′ 的初始状态。
步骤 3 - 然后对于 Q1 中的每个状态 q 执行以下操作：添加此新状态，将 δ(q,a)=∪pϵqδ(p,a) 添加到 δ 中，其中右侧的 δ 是 NFA M′ 的 δ。
步骤 4 - 重复步骤 3 直到有新状态需要添加到 Q1 中，如果有要添加到 Q1 中的新状态，则过程终止。
示例 4 - 证明如果 L 被具有 ∈-转移的 NFA 接受，则 L 被不具有 ∈-转移的 NFA 接受。
解决方案
假设 L = L (D) 对于某些不具有 ∈-转移的 DFA 或 NFA。可以通过为 D 的所有状态 q 添加转移 δ(q,∈)=ф 来将其转换为 ∈-DFA (E)。还可以将 D 上输入符号的转移例如 δD(q,a)=D 移动到 NFA 转移到仅包含 P 的集合中，即 δE(q,a)={P}。因此，E 和 D 的转移是相等的，但 E 明确指出 E 的任何状态都没有转移。
令 E=(QE,Σ,δE,q0,FE) 为 ∈-NFA。可以使用上面表示的修改后的子集构造来创建 DFA。
D=(QE,∑,δE,qD,FD)
L(D)=L(E)，因为 E 和 D 的扩展转移函数是相等的。扩展转移函数是取状态 q 和字符串 w 并返回状态 P 的函数，即自动机在从状态 q 开始并处理输入序列 w 时到达的状态。
δE(q0,w)=δD(qD,w) 通过对 w 的长度进行归纳。
2K+ 次查看
