什么是确定性有限自动机 (DFA)？

确定性意味着对于每个输入，自动机只有一个状态可以从其当前状态转换。在确定性有限自动机中，磁头只能沿一个方向移动以扫描输入磁带符号。但在双向有限自动机的情况下，在扫描输入符号时，磁带的磁头可以从其当前位置向右或向左移动。

确定性有限自动机是一组 5 元组，定义为

M=(Q,Σ,δ,q₀,F)，其中：

• Q：有限控制中存在的非空有限状态集 (q₀,q₁,q₂)。

• Σ：非空有限的输入符号集。

• δ：这是一个转移函数，它接受两个参数，一个状态和一个输入符号，它返回一个由∴ δ：Q x Σ →Q 表示的单个状态。设 q 为状态，a 为传递给转移函数的输入符号。δ(q,a)=q。q 是函数的输出，它可能是相同的状态或新的状态。

• q₀ ∈ Q 是初始状态。

• F⊆ Q 是最终状态集。

示例 - 最小化以下 DFA

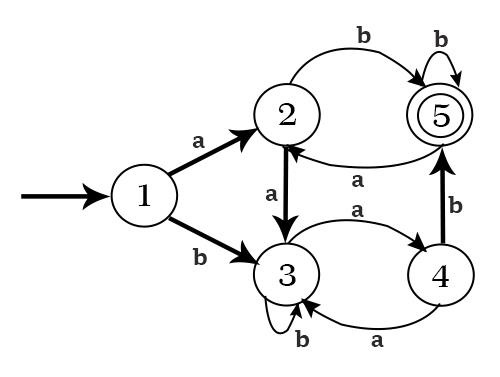
解决方案

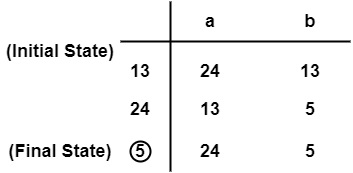
• 制作一个状态转移表。

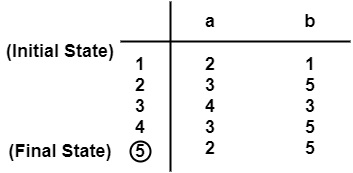
• π₀= {{5}}, {1, 2, 3, 4}}
• 对于输入 a，在 π₀ 的 {1, 2, 3, 4} 上

• 对于输入 b，在 π₀ 的 {1, 2, 3, 4} 上

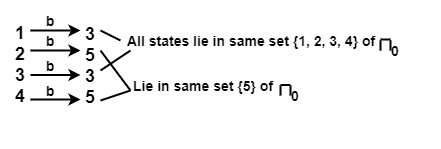
∴ {1, 2, 3, 4} 将被分成 {1, 3} 和 {2, 4}

∴ π₁={{5},{1,3},{2,4}}

• 对于 π₁ 的 {1, 3} 上的输入符号 a

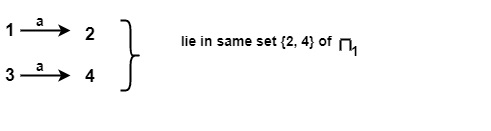
同样对于 π₁ 的 {2, 4} 上的输入符号 a

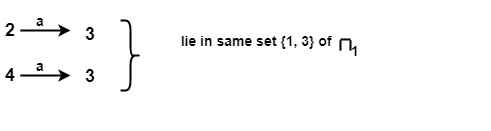
• 对于 π₁ 的 {1, 3} 上的输入符号 b

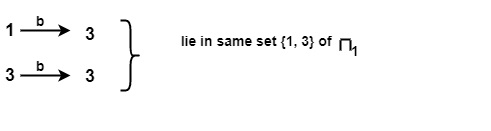
同样对于 π₁ 的 {2, 4} 上的输入符号 b

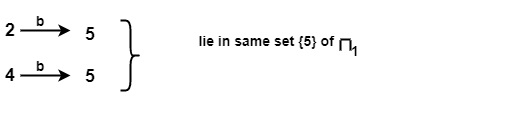
π₁ 中的子集，即 {1, 3} 和 {2, 4} 将不会被分割。

π_final= {{5}, {1, 3}, {2, 4}}

DFA 将有 3 个状态。

{5}, {1, 3} 和 {2, 4}

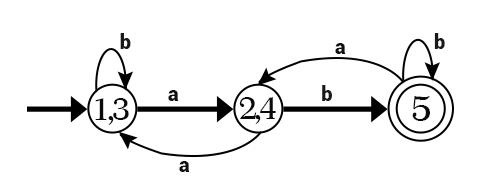
最小化的 DFA 将是 -

Ginni

更新于：2021年10月26日

2K+ 次查看

启动您的职业生涯

通过完成课程获得认证

开始