构造一个接受在字母表 {0,1} 上的偶长度回文串的图灵机 (TM)？

图灵机 (TM) 是一个 7 元组 (Q, ∑, Γ, δ, q0, qaccept , qreject)。

其中，

  • Q 是一个有限的状态集。

  • ∑ 是输入字母表，不包含空白符号 t。

  • Γ 是带字母表，其中 t ∈ Γ 且 ∑ ⊆ Γ。

  • δ: (Q × Γ) → (Q × Γ × {L, R}) 是转移函数。

  • q0 ∈ Q 是起始状态。

  • qaccept ∈ Q 是接受状态。

  • qreject ∈ Q 是拒绝状态，其中 qreject ≠ qaccept。

**为了接受在字母表 {0,1} 上的偶长度回文串，**请按照以下步骤操作 -

  • 匹配第一个和最后一个元素并擦除它们，继续执行相同的操作。一旦我们在没有任何不匹配的情况下到达空串，则该字符串是偶长度回文串。

  • 对于偶长度回文串，在机器运行并擦除第一个和最后一个元素且没有遇到不匹配后，定义了一个 TM。之后，图灵机接受该字符串，该字符串是偶长度回文串。

假设字符串为 -

110011

那么，我们可以遇到三种情况，如下所示 -

**情况 1** - 如果起始和结束匹配，则擦除第一个和最后一个

擦除后 - 1001

**情况 2** - 如果起始和结束匹配，则擦除第一个和最后一个

擦除后 - 00

**情况 3** - 如果起始和结束匹配，则擦除第一个和最后一个零

擦除后剩余 - 空串

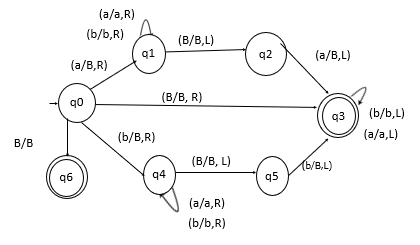
这是一个构造的图灵机，它接受偶长度回文串。

接受偶回文串的 TM 的示意图如下所示 -

更新于: 2021年6月16日

9K+ 浏览量

开启你的 职业生涯

通过完成课程获得认证

立即开始
广告