数据结构
网络
关系型数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学构造一个确定性有限自动机 (DFA)，识别在字母表∑={0,1} 上的语言 {x | 1 的个数能被 2 整除，且 0 的个数能被 3 整除}。
问题
给定的语言 L={ x | 1 的个数能被 2 整除，且 0 的个数能被 3 整除}，字母表 ∑={0,1}。
解答
该语言分为两部分，首先我们需要找到 1 的个数能被 2 整除的情况，其次找到 0 的个数能被 3 整除的情况，最后将两部分结合起来生成结果。
步骤 1 - 第一部分的 DFA，1 的个数能被 2 整除。
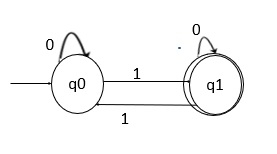
这里：
q0 状态下输入 0 转到 q0（最终状态），生成字符串 0，被该语言接受。
q0 状态下输入 1 转到 q1，q1 状态下输入 1 转到 q0（最终状态），生成字符串 “11”，个数能被 2 整除。
q0 状态下输入 0 转到 q0，q0 状态下输入 1 转到 q1，q1 状态下输入 0 转到 q1，q1 状态下输入 1 转到 q0（最终状态），生成字符串 “0101”，个数能被 2 整除。
步骤 2 - 第二部分的 DFA，0 的个数能被 3 整除。
这里：
q0’ 状态下输入 1 转到 q0’（最终状态），生成字符串 1，被该语言接受。
q0’ 状态下输入 0 转到 q1’，q1’ 状态下输入 0 转到 q2’，q2’ 状态下输入 0 转到 q0’（最终状态），生成字符串 “000”，个数能被 3 整除。
步骤 3 - 最终的 DFA 是：第一部分 DFA × 第二部分 DFA。
| 状态 | 0 | 1 |
|---|---|---|
| {q0q0’} | {q0q1’} | {q1q0’} |
| {q0q1’} | {q0q2’} | {q1q1’} |
| {q0q2’} | {q0q0’} | {q1q2’} |
| {q1q0’} | {q1q1’} | {q0q0’} |
| {q1q1’} | {q1q2’} | {q0q1’} |
| {q1q2’} | {q1q0’} | {q0q2’} |
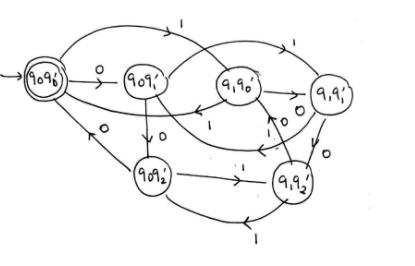
状态转换图
DFA 的状态转换图如下所示：
更新于：2021年6月15日
4K+ 次浏览
广告