数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究构建交替出现 0 和 1 的 DFA
问题
构建一个确定性有限自动机 (DFA)，其语言由在字母表 ∑ ={0,1} 上交替出现 0 和 1 的字符串组成。
解决方案
If Σ = {0, 1}
(ε + 1)(01)*
(ε + 0) is the set of strings that alternate 0’s and 1’s
Another expression for the same language is (01)*+ 1(01)*+ (01)*0+ 1(01)*0.给定语言生成的字符串如下所示：
如果没有输入是 0 或 1，则它生成 {ε}。
字符串以 0 开头，后跟 1 = {0101…}。
字符串以 1 开头，后跟 0 ={101010….. }
因此，根据字符串生成，可以清楚地看出字符串以 ε、(01)*、(10)* 开头，但没有限制字符串只能以 0 或 1 开头，因此考虑到所有这些点，满足给定语言中交替出现 0 和 1 的表达式为：
(01)* + (10)* + 0(10)* + 1(01)*
DFA
给定语言的 DFA 为：
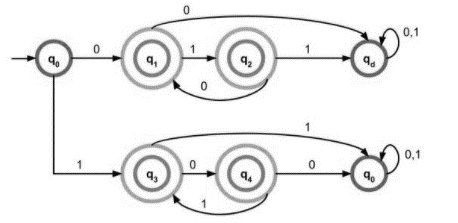
解释
从初始状态开始，它生成的字符串，q0 上的 0 转到 q1，它是最终状态之一，只接受 0，满足给定条件。
从初始状态开始，它生成的字符串，q0 上的 1 转到 q3，它是最终状态之一，只接受 1，满足给定条件。
q0 达到最终状态 q2，它生成字符串“01”，该字符串被语言接受。
q0 达到最终状态之一 q4，它生成字符串“10”，该字符串被语言接受。
类似地，DFA 也接受其余字符串。
更新于： 2021年6月15日
3K+ 浏览量
广告