设计一个接受奇数个 0 或偶数个 1 的 DFA 机器
确定性有限自动机 (DFA) 是一个五元组
M=(Q, Σ, δ,q0,F)
其中,
- Q:称为状态的有限集。
- Σ:称为字母表的有限集。
- δ:Q × Σ → Q 是转移函数。
- q0 ϵ Q 是起始或初始状态。
- F:最终或接受状态。
问题
构造一个接受奇数个 0 或偶数个 1 的 DFA 机器。
解决方案
针对字母表 Σ={0,1} 上的两个条件设计两个独立的机器 -
仅接受奇数个 0 的 DFA
仅接受偶数个 1 的 DFA
在字母表 Σ={0,1} 上仅接受奇数个 1 的 DFA
语言 L= {1,10,1110,1011,10101,100101,….}
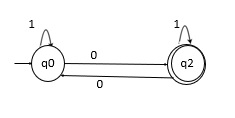
在字母表 Σ={0,1} 上仅接受偶数个 1 的 DFA
语言 L= {11,101,11110,10111,101101,1001011,….}
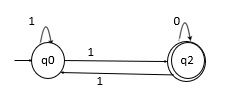
现在合并两个状态转换图以生成一个接受奇数个 0 或偶数个 1 的机器
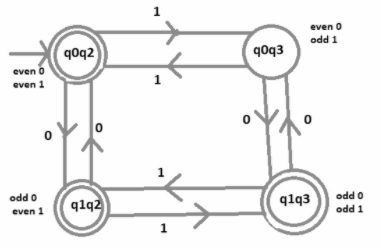

广告

 数据结构
数据结构 网络
网络 关系数据库管理系统
关系数据库管理系统 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 编程
C 编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP