数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究用C++构建用于L = {a(2*m)c(4*n)dnbm | m,n = 0}的下推自动机
给定一种语言“L”，任务是为该语言构建一个下推自动机。该语言规定字符'a'的出现次数应为字符'b'出现次数的两倍，字符'c'的出现次数应为字符'd'出现次数的四倍，所有字符的出现次数至少为1，也允许空字符串，并且空字符串应被自动机接受。
什么是下推自动机？
下推自动机 (PDA) 是一种实现上下文无关文法的技术，类似于我们为正则文法设计确定性有限自动机 (DFA) 的方式。DFA 可以操作有限数据，而 PDA 可以操作无限数据。我们可以将下推自动机理解为“有限状态机”和“栈”的组合。
下推自动机有三个组成部分：
输入带；
控制单元；以及
大小无限的栈。
PDA 可以正式地描述为一个 7 元组 (Q, Σ, S, δ, q0, I, F)：
Q 是有限数量的状态
Σ 是输入字母表
S 是栈符号
δ 是转移函数：Q × (Σ υ {ε}) × S × Q × S*
q0 是初始状态 (q0 Ε Q)
I 是初始栈顶符号 (I Ε S)
F 是一组接受状态 (F Ε Q)
让我们为给定的语言构建一个下推自动机：
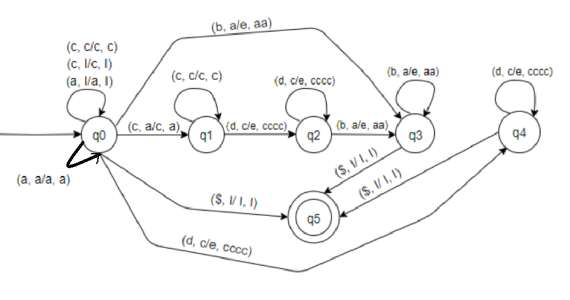
这个 PDA 接受的字符串形式为：
c4ndn − ccccd，cccccccccdd 等。c 的数量是 d 的数量的 4 倍。当 m 为 0 时，将没有 a 和 b。不断压入 c，一旦遇到第一个 d，就从栈中弹出 4 个 c。如果到达字符串末尾并且没有剩余的 c，则接受该字符串。
a2mbm − aab，aaaabb 等。a 的数量是 b 的数量的两倍。当 n 为 0 时，将没有 c 和 d。不断压入 a，一旦遇到第一个 b，就从栈中弹出 2 个 a。如果到达字符串末尾并且没有剩余的 a，则接受该字符串。
a2mc4ndnbm − aaccccdb，aaaaccccccccddbb 等。a 的数量是 b 的数量的两倍，c 的数量是 d 的数量的四倍。不断压入 a 和 c。一旦遇到第一个 d，就弹出 4 个 c（如果在栈顶），然后为剩余的 b 弹出 2 个 a。如果到达字符串末尾并且没有剩余的 a，则接受该字符串。
空字符串也被接受：a0c0d0b0。
让我们理解这个机器
状态 q0 的转移：
( a, I/a,I ) − 如果栈顶是 I 且当前输入符号是 a，则将 a 压入栈顶并保持在 q0。栈变为 aI…
( c, I/c,I ) − 如果栈顶是 I 且当前输入符号是 c，则将 c 压入栈顶并保持在 q0。栈变为 cI…
( a, a/a,a ) − 如果栈顶是 a 且当前输入符号也是 a，则将 a 压入栈顶并保持在 q0。栈变为 aa… 继续压入 a 直到下一个 c 或 b。
( c, c/c,c ) − 如果栈顶是 c 且当前输入符号也是 c，则将 c 压入栈顶并保持在 q0。栈变为 cc… 继续压入 c 直到下一个 d。
( b, a/e,aa ) − 如果栈顶是 a 且当前输入符号是 b，则从栈中弹出 2 个 a 并移动到 q3。
(c, a/c,a ) − 如果栈顶是 a 且当前输入符号是 c，则将 c 压入栈顶并移动到 q1。栈变为 ca…
( d, c/e,cccc ) − 如果栈顶是 c 且当前输入符号是 d，则从栈中弹出 4 个 c 并移动到 q4。
( $, I/I, I) − 如果栈顶是 I 且没有输入，则什么也不做并移动到 q5。用于空字符串。
状态 q1 的转移：
( c, c/c,c ) − 如果栈顶是 c 且当前输入符号也是 c，则将 c 压入栈顶并保持在 q1。栈变为 cc… 继续压入 c 直到下一个 d。
( d, c/e,cccc ) − 如果栈顶是 c 且当前输入符号是 d，则从栈中弹出 4 个 c 并移动到 q2。
状态 q2 的转移：
( d, c/e,cccc ) − 如果栈顶是 c 且当前输入符号是 d，则从栈中弹出 4 个 c 并移动到 q2。
( b, a/e,aa ) − 如果栈顶是 a 且当前输入符号是 b，则从栈中弹出 2 个 a 并移动到 q3。
状态 q3 的转移：
( b, a/e,aa ) − 如果栈顶是 a 且当前输入符号是 b，则从栈中弹出 2 个 a 并保持在 q3。
( $, I/I, I ) − 如果栈顶是 I 且没有输入，则什么也不做并移动到 q5。用于空字符串。
状态 q4 的转移：
( d, c/e,cccc ) − 如果栈顶是 c 且当前输入符号是 d，则从栈中弹出 4 个 c 并保持在 q4。
( $, I/I, I ) − 如果栈顶是 I 且没有输入，则什么也不做并移动到 q5。用于空字符串。
496 次浏览
