数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究构建用于 anbmc(n+m) (n,m≥1) 的 DPDA（在 TOC 中）
下推自动机 (PDA) 可以用七元组的形式描述
(Q, Σ,S, δ,q0,I,F)
其中，
- Q 是有限数量的状态
- Σ 是输入字母表
- S 是栈符号
- Δ 是转移函数：QX(ΣU{e})XSXQ
- q0 是初始状态 (q0 属于 Q)
- I 是初始栈顶符号
- F 是一个接受状态集 (F 属于 Q)
问题
构建用于 **anbmc(n+m)** (n,m≥1) 的 PDA
解决方案
因此，由给定语言生成的字符串如下：
L={abcc,aabccc,aaabbccccc,….}
也就是说，将 a 的数量和 b 的数量相加，其结果将等于 c 的数量。
因此，对于每个 a 和 b，我们将从栈中弹出 c。让我们统计 a 和 b 的数量，总数量等于 c 的数量。可以通过将 a 和 b 推入栈中，然后在遇到 "c" 时弹出 a 和 b 来实现。
最后，如果字符串末尾栈中没有任何内容，那么我们可以说 PDA 接受了该语言。
给定问题的 PDA 如下：
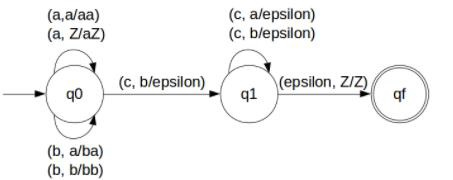
转移函数
转移函数如下：
步骤 1：δ(q0, a, Z) = (q0, aZ)
步骤 2：δ(q0, a, a) = (q0, aa)
步骤 3：δ(q0, b, a) = (q0, ba)
步骤 4：δ(q0, b, b) = (q0, bb)
步骤 5：δ(q0, c, b) = (q1, ε)
步骤 6：δ(q1, c, b) = (q1, ε)
步骤 7：δ(q1, c, a) = (q1, ε)
步骤 8：δ(q1, ε, Z) = (qf, Z)
解释
**步骤 1** - 让我们取输入字符串："aabbcccc"，它满足给定条件。
**步骤 2** - 从左到右扫描字符串。
**步骤 3** - 对于输入 'a' 和栈字母 Z，则：
将输入 'a' 推入栈中：(a,Z/aZ)，状态将为 q0
**步骤 4** - 对于输入 'a' 和栈字母 'a'，则：
将输入 'a' 推入栈中：(a,a/aa)，状态将为 q0
**步骤 5** - 对于输入 'b' 和栈字母 'a'，则：
将输入 'b' 推入栈中：(b,a/ba)，状态将为 q0
**步骤 6** - 对于输入 'b' 和栈字母 'b'，则：
将输入 'b' 推入栈中：(b,b/bb)，状态将为 q0
**步骤 7** - 对于输入 'c' 和栈字母 'b' 以及状态为 q0，则：
弹出 'b'：(c,b/ε)，状态将为 q1
**步骤 8** - 对于输入 'c' 和栈字母 'b' 以及状态为 q1，则：
弹出 'b'：(c,b/ε)，状态保持为 q1
**步骤 9** - 对于输入 'c' 和栈字母 'a' 以及状态为 q1，则：
弹出 'a'：(c,a/ε)，状态将为 q1
**步骤 10** - 对于输入 'c' 和栈字母 'a' 以及状态为 q1，则：
弹出 'a'：(c,a/ε)，状态将保持为 q1
**步骤 11** - 我们到达了字符串的末尾，对于输入 ε 和栈字母 Z，则：
转到最终状态(qf)：(ε, Z/Z)
1K+ 浏览量
