数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究使用 C++ 构建用于语言 L = {an bm a(n+m) - n,m≥1} 的图灵机
图灵机 - 图灵机是一种用于接受由 0 型文法生成的语言的单词的设备。图灵机 (TM) 是一种数学模型，它由一条无限长的带组成，带被分成单元格，输入在这些单元格上给出。它包括一个读取输入带的磁头。状态寄存器存储图灵机的状态。读取输入符号后，将其替换为另一个符号，其内部状态发生变化，并且它从一个单元格向右或向左移动。如果 TM 达到最终状态，则接受输入字符串，否则拒绝。
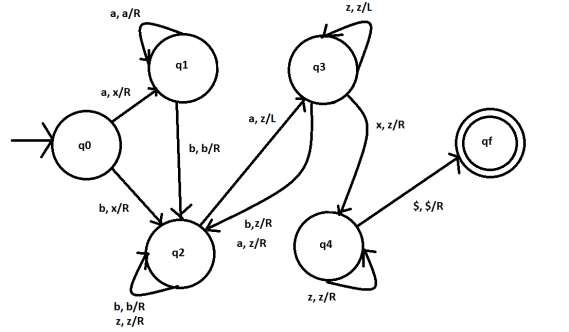
TM 可以正式描述为一个 7 元组 (Q, X, Σ, δ, q0, B, F)，其中 -
- Q 是有限的状态集
- X 是带字母表
- Σ 是输入字母表
- δ 是转移函数；δ : Q × X → Q × X × {左移，右移}。
- q0 是初始状态
- B 是空白符号
- F 是最终状态集
我们的目标是构建一个接受语言的图灵机 TM
L= anbma(n+m) 其中 n,m>=1
让我们举一些 TM 可以接受的单词的例子，
- abaa，n=1，m=1
- aabaaa，n=2，m=1
- abbaaa，n=1，m=2
- aaabaaaa，n=3，m=1
也就是说，n 个 a 后跟 m 个 b，然后再跟 n+m 个 a。n,m>=1
a 的最小数量始终为 3，b 为 1。当 n=m=1 时。
方法总结如下：
机器首先接受所有 n 个 a，然后接受所有 m 个 b。然后，随着遇到更多 a，它开始删除之前的输入 b 和 a。最后，当没有新的 a 并且磁头到达第一个输入字符时，这意味着所有字符都已正确处理。让我们逐步按照输入字符串进行操作：
从状态 q0 开始的转换
δ (q0, a) → ( q1, x, R )。在状态 q0，如果读取的字符是 a，则转换到状态 q1，将其设为 x 并向右移动以指向字符串中的下一个字符。
例如 - aabaaa → xabaaa（第一个字符变为 x，磁头向右移动到下一个 a）
δ ( q0, b ) → ( q3, x, R )。在状态 q0，如果读取的字符是 a，则转换到状态 q3，将其设为 x 并向右移动以指向字符串中的下一个字符。
例如 - babaaa…. → xabaaa….（第一个字符变为 x，磁头向右移动到下一个 a）
这里 x 用于表示第一个字符。
从状态 q1 开始的转换
δ ( q1, a ) → ( q1, a, R )。在状态 q1，如果读取的字符是 a，则保持在状态 q1，并向右移动以指向字符串中的下一个字符。
例如：xaabaaa… → xaabaaa…（对于其余的 a，不做任何操作并向右移动）
δ ( q1, b ) → ( q2, b, R )。在状态 q1，如果读取的字符是 b，则保持在状态 q1，并向右移动以指向字符串中的下一个字符。
例如 - xaabaaa… → xaabaaa…（对于其余的 b，不做任何操作并向右移动）
从状态 q2 开始的转换
δ ( q2, b ) → ( q2, b, R )。在状态 q2，如果读取的字符是 b，则保持在状态 q2，并向右移动以指向字符串中的下一个字符。
例如 - xaabbbaaa… → xaabbbaaa…（对于其余的 b，不做任何操作并向右移动）
δ ( q2, z ) → ( q2, z, R )。在状态 q2，如果读取的字符是 z，则保持在状态 q2，并向右移动以指向字符串中的下一个字符。
例如 - xaabaazz… → xaabaazz…（对于其余的 z，不做任何操作并向右移动）
δ ( q2, a ) → ( q3, z, L )。在状态 q2，如果读取的字符是 a，则将其设为 z，然后转换到状态 q3，并向左移动以指向字符串中的上一个字符。
例如 - xaabaazz… → xaabazzz…（对于 a，用 z 替换并向左移动）
从状态 q3 开始的转换
δ ( q3, z ) → ( q3, z, L )。在状态 q3，如果读取的字符是 z，则保持在状态 q3，并向左移动以指向字符串中的上一个字符。
例如 - xaabzzzz… → xaabzzzzz…（对于 z，不做任何操作并向左移动）
δ ( q3, b ) → ( q2, z, R )。在状态 q2，如果读取的字符是 b，则将其设为 z 并转换到状态 q2，并向右移动以指向字符串中的下一个字符。替换所有 b。
例如 - xaabzzzz… → xaazzzzz…（对于 b，用 z 替换并向右移动）
δ ( q3, a ) → ( q2, z, R )。在状态 q2，如果读取的字符是 a，则将其设为 z 并转换到状态 q3，并向右移动以指向字符串中的下一个字符。替换所有 a。
例如 - xaazzzz… → xaazzzzz…（对于 a，用 z 替换并向右移动）
δ ( q3, x ) → ( q4, z, R )。在状态 q2，如果读取的字符是 x，则将其设为 z，然后转换到状态 q3，并向右移动以指向字符串中的下一个字符。第一个符号已到达。
例如 - xzzzzzzz… → zzzzzzzz…（对于 x，用 z 替换并向右移动）
从状态 q4 开始的转换
δ ( q4, z ) → ( q4 z, R )。在状态 q4，如果读取的字符是 z，则保持在状态 q4，并向右移动以指向字符串中的下一个字符。现在所有字符都是 z。
例如 - zzzzzzzz… → zzzzzzzz…（对于所有 z，不做任何操作并向右移动）
δ ( q4, $ ) → ( qf, $ , R )。在状态 q4，如果不再有字符，则到达末尾。转换到最终状态 qf。这意味着字符串被接受。
例如 - zzzzzzzz$ → zzzzzzzz（对于字符串的结尾，$ 不做任何操作并移动到最终状态）
图表显示了图灵机 -
输入
aabaaa q0: aabaaa → q1: xabaaa → q1: xabaaa → q2: xabaaa → q3: xabzaa → q2: xazzaa q2: xazzaa → q3: xazzza → q3: xazzza → q3: xazzza → q2: xzzzzza → q2: xzzzzza q2: xzzzzza → q2: xzzzzza → q2: xzzzzza → q2: xzzzzzz → q3: xzzzzzz…….. q3: xzzzzzz → q3: xzzzzzz → q4: zzzzzzz → q4: zzzzzzz…….q4: xzzzzzz$ → qf: xzzzzzz$
到达 qf 意味着 aabaaa 被接受
2K+ 次浏览
