数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究构建一个用于 L = {a^n b^n | n>=1} 的图灵机。
图灵机 (TM) 比有限自动机 (FA) 和下推自动机 (PDA) 都更强大。它们的强大程度与我们迄今为止构建的任何计算机一样。
图灵机的形式化定义
图灵机可以形式化地描述为七元组
(Q,X, Σ, δ,q0,B,F)
其中，
Q 是有限的状态集
X 是带字母表
Σ 是输入字母表
δ 是转移函数：δ:QxX→QxXx{左移，右移}
q0 是初始状态
B 是空白符号
F 是最终状态。
图灵机 (TM) 是一种数学模型，它由一条无限长的带组成，该带被分成单元格，输入在这些单元格上给出。它包含一个读取输入带的读写头。一个状态寄存器存储图灵机的状态。
读取输入符号后，它会被替换为另一个符号，其内部状态发生变化，并且它从一个单元格向右或向左移动。如果 TM 达到最终状态，则接受输入字符串，否则拒绝。
图灵机有一个读/写头。所以我们可以在磁带上写入。
现在，让我们构建一个接受相同数量的 a 和 b 的图灵机，
它生成的语言是 L ={ anbn | n>=1}，给定语言接受的字符串为 -
L= {ab, aabb, aaabbb, aaaabbbb,………}
示例
考虑 n=3，所以 a3b3，磁带看起来像 -
B= 空白
我们需要将每个 'a' 转换为 X，并将每个 'b' 转换为 Y。如果图灵机包含相等数量的 X 和 Y，则它将到达最终状态。
步骤 1 - 将初始状态视为 q0。此状态将 'a' 替换为 X 并向右移动，现在状态从 q0 更改为 q1，因此转移函数为 -
δ(q0, a) = (q1,X,R)
步骤 2 - 向右移动，直到看到空白符号。
δ(q1, a) = (q1,a,R) δ(q1, b) = (q1,b,R)
到达空白符号 B 后，向左移动并将状态更改为 q2，因为我们需要将最后一个 'b' 更改为 Y。
δ(q1, B) = (q2,B,L) //1st iteration δ(q1, Y) = (q2,Y,L) // remaining iterations
步骤 3 - 当我们看到符号 'b' 时，将其替换为 Y 并将状态更改为 q3 并向左移动。
δ(q2, B) = (q3,Y,L)
步骤 4 - 向左移动直到到达符号 X。
δ(q3, a) = (q3,a,L) δ(q3, b) = (q3,b,L)
当我们到达 X 时，向右移动并将状态更改为 q0，并开始下一次迭代。
在通过将状态从 q0 更改为 q4 将每个 'a' 和 'b' 替换为 X 和 Y 后，我们得到以下结果 -
δ(q0, Y) = (q4,Y,N)
N 表示不动。
| X | X | X | Y | Y | Y | B | B | ....................... |
q4 是图灵机的最终状态，q0 是图灵机的初始状态，中间状态为 q1、q2、q3。
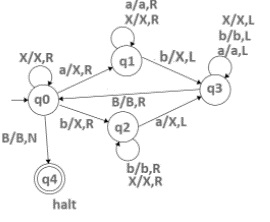
转移图
图灵机的转移图如下 -
23K+ 浏览量
