数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究构建用于减法的图灵机
图灵机是一个七元组
(Q, Σ,Γ, δ,q0,qacc, qrej)
其中，
- Q 是有限数量的状态
- Σ 是输入字母表，不包含空白符号 t；
- Γ 是带字母表，其中 t ε Γ 且 Σ ⊆ Γ；
- δ: (Q × Γ) → (Q × Γ × {L, R}) 是转移函数；
- q0 ε Q 是起始状态；
- qacc ε Q 是接受状态；
- qrej ε Q 是拒绝状态，其中 qrej ≠qacc。
问题
构建一个用于两个一元整数减法的图灵机 (TM)。
解决方案
两个一元整数的减法
3-2=1
在图灵机中，3 表示 - 111
2 表示：11
令 'M' 为用于分隔两个整数的符号
| B | 1 | 1 | 1 | M | 1 | 1 | B |
这里 B= 空白
M= 用于分隔两个整数的符号
算法
按照以下分步算法构建用于减法的 TM：
步骤 1 - 将两个一元整数作为输入。我们从初始状态 q0 开始。
步骤 2 - 如果我们在字符串中找到 1，则转到相同的状态，不更改 1 的值，并转到字符串的右侧。
步骤 3 - 如果我们找到 m 符号，则忽略此符号，不更改符号，并转到字符串的右侧。
步骤 4 - 如果我们在经过 M 符号后找到 1，则将 1 的值更改为 X 并转到字符串的左侧。
步骤 5 - 然后经过 M 符号并向左移动，如果我们找到 1，则将 1 的值更改为 X 并向右移动。
步骤 6 - 因此，在符号 (M) 之后，我们将所有 1 的值更改为 X，并且在符号 M 之前将相同数量的 1 更改为 X。
步骤 7 - 应用这些步骤并获得两个一元整数减法的图灵机。
在处理减法时，图灵机根据用户提供的输入考虑三种情况中的任何一种。
如果 'a' 和 'b' 是两个整数，我们需要考虑：
- a>b
- a<b
- a=b
通过考虑所有三种情况，最终的图灵机如下所示：
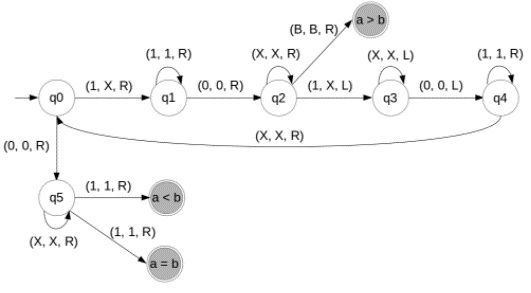
图解说明
步骤 1 - 将输入字符串视为 110111
即 a=11 且 b=111，根据给定的输入 a
步骤 2 - 从左到右扫描字符串。
步骤 3 - 将 '1' 标记为 'X'，然后向右移动。
步骤 4 - 到达 '0' 的右侧，并将 '1' 标记为 'X'，然后向左移动。
步骤 5 - 到达 '0' 左侧的 'X'，然后向右移动一步。
步骤 6 - 再次将 '1' 标记为 'X'，然后向右移动。
步骤 7 - 到达 '0' 的右侧并经过 'X'，将 '1' 标记为 'X'，然后向左移动。
步骤 8 - 到达 '0' 左侧的 'X'，然后向右移动一步。
步骤 9 - 如果 'X' 之后存在 '0'，则表示 '0' 之前的 '1' 都已完成。
步骤 10 - 经过 '0'、'X'，并且还有 '1' 剩余。也就是说，第二个数字大于第一个数字。
步骤 11 - 然后最终状态为“a<b”
9K+ 浏览量
