如果三条直线l、m、n满足l∥m且n⊥l，证明n⊥m。

已知

l、m、n是三条直线，满足l∥m且n⊥l。

要求

我们必须证明n⊥m。

解答

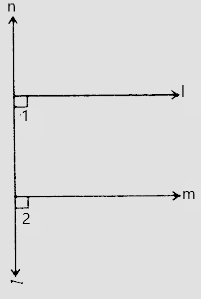
n⊥l

这意味着：

∠1 = 90°

l∥m，n是横截线。

因此：

∠1 = ∠2 (同位角相等)

∠2 = 90°

这意味着：

n⊥m。

证毕。

教程点

更新于：2022年10月10日

浏览量：101

开启你的职业生涯

完成课程获得认证

开始学习