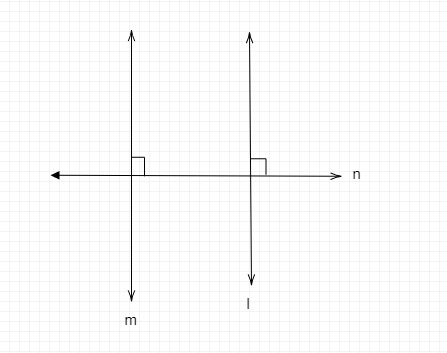
如果直线 $m \perp n$ 且 $n \perp l$，那么关于直线 $m$ 和 $l$ 的关系可以说什么？
已知
直线 $m$ 垂直于直线 $n$。
直线 $n$ 垂直于直线 $l$。
求解
我们需要找到直线 $m$ 和 $l$ 之间的关系？
解答
直线 $m$ 垂直于直线 $n$。
直线 $n$ 垂直于直线 $l$。
这意味着，
直线 $m$ 和 $l$ 互相平行。
- 相关文章
- 如果 $l, m, n$ 是三条直线，使得 $l \parallel m$ 且 $n \perp l$，证明 $n \perp m$。
- 如果 \( a=x^{m+n} y^{l}, b=x^{n+l} y^{m} \) 且 \( c=x^{l+m} y^{n} \)，证明 \( a^{m-n} b^{n-1} c^{l-m}=1 . \)
- 如果 \( x=a^{m+n}, y=a^{n+1} \) 且 \( z=a^{l+m} \)，证明 \( x^{m} y^{n} z^{l}=x^{n} y^{l} z^{m} \)
- 化简：\( \sqrt[lm]{\frac{x^{l}}{x^{m}}} \times \sqrt[m n]{\frac{x^{m}}{x^{n}}} \times \sqrt[n l]{\frac{x^{n}}{x^{l}}} \)
- 为 L = {0n1m2(n+m) | m,n >=1} 构造 PDA。
- 如果 $l+m+n=9$ 且 $l^2+m^2+n^2=31$，则求 $lm + mn + nl$ 的值。
- 求下列式子的和：$l^{2}+m^{2}, m^{2}+n^{2}, n^{2}+l^{2}, 2lm+2mn+2nl$
- 在图中，\(P A \) 和 \( P B \) 是从外一点 \( P \) 到以 \( O \) 为圆心的圆的切线。\( L N \) 与圆在 \( M \) 点相切。证明 \( P L+L M=P N+M N \)。
- 用 C++ 构造 L = {0n1m2(n+m) | m,n = 0} 的下推自动机。
- 因式分解$(l+m)^{2}-(l-m)^{2}$
- 用 C++ 构造 L = {0(n+m)1m2n | m, n = 0} 的下推自动机。
- 用 C++ 构造 L = {0m1(n+m)2n | m,n = 0} 的下推自动机。
- 因式分解表达式：$( l+m)^2-( l-m)^2$。
- 用 C++ 构造 L = {an bm a(n+m) - n,m≥1} 的图灵机。
- 设 $l$ 为一条直线，$P$ 为不在 $l$ 上的一点。过 $P$ 作一条平行于 $l$ 的直线 $m$。现在连接 $P$ 到 $l$ 上的任意一点 $Q$。在 $m$ 上选择任意其他一点 $R$。过 $R$ 作一条平行于 $PQ$ 的直线。设这条直线与 $l$ 相交于 $S$。这两组平行线围成的图形是什么？
开启你的 职业生涯
通过完成课程获得认证
开始学习
数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装设计
法律研究