设l是一条直线,P是不在l上的一个点。过P点作一条与l平行的直线m。现在连接P到l上任意一点Q。在m上选择另一个点R。过R点作一条与PQ平行的直线。设这条直线与l相交于点S。这两组平行线围成的图形是什么形状?
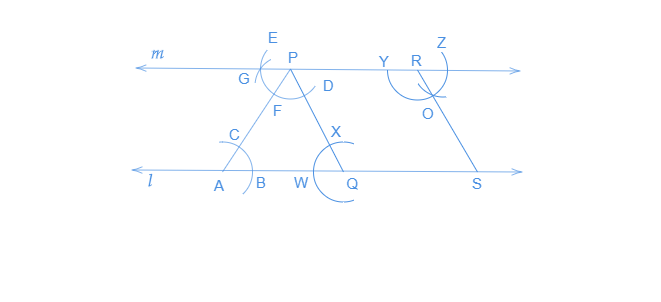
作图步骤
- 画一条直线l,在其上取一点A。
- 取一点P,不在l上,连接A到P。
- 以A为圆心,用适当的半径画弧,与l相交于B,与AP相交于C。
- 以P为圆心,用与前面相同的半径画弧DE,与AP相交于F。
- 调整圆规到BC的长度,保持圆规开口不变,以F为圆心,画弧与前面画的弧DE相交于点G。
- 连接P到点G画一条直线m。直线m将平行于l。
- 连接P到直线l上的任意一点Q。在直线m上选择另一点R。
- 同样地,可以使用上述步骤过R点画一条平行于PQ的直线。设它与直线l相交于点S。
因此,直线PQ平行于RS。这两组平行线围成的图形是平行四边形PQRS,其中PR平行于QS,PQ平行于RS。

广告

 数据结构
数据结构 网络
网络 关系数据库管理系统(RDBMS)
关系数据库管理系统(RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C语言编程
C语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP