设P是角∠ABC的角平分线上的一个点。如果过P且平行于AB的直线交BC于Q,证明三角形BPQ是等腰三角形。
已知
P是角∠ABC的角平分线上的一个点。过P且平行于AB的直线交BC于Q。
要求
我们必须证明BPQ是等腰三角形。
解答
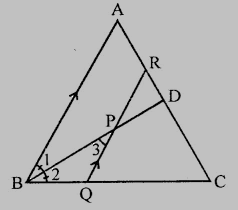
根据图形,
BD是CB的角平分线
这意味着,
∠1=∠2......(i)
RQ∥AB
这意味着,
∠1=∠3.......(ii) (内错角)
由(i)和(ii)可得,
∠2=∠3
这意味着,
PQ=BQ (等角对等边)
因此,△BPQ是等腰三角形。

广告
已知
P是角∠ABC的角平分线上的一个点。过P且平行于AB的直线交BC于Q。
要求
我们必须证明BPQ是等腰三角形。
解答

根据图形,
BD是CB的角平分线
这意味着,
∠1=∠2......(i)
RQ∥AB
这意味着,
∠1=∠3.......(ii) (内错角)
由(i)和(ii)可得,
∠2=∠3
这意味着,
PQ=BQ (等角对等边)
因此,△BPQ是等腰三角形。
