$\triangle ABC$是一个三角形，过$A, B, C$分别作与$BC, CA$和$AB$平行的直线，交于$P, Q$和$R$。证明$\triangle PQR$的周长是$\triangle ABC$周长的两倍。

已知

$\triangle ABC$是一个三角形，过$A, B, C$分别作与$BC, CA$和$AB$平行的直线。

要求

我们必须证明$\triangle PQR$的周长是$\triangle ABC$周长的两倍。

解答

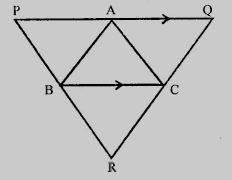
$PQ \parallel BC$ 且 $QR \parallel AB$

这意味着，

$ABCQ$是一个平行四边形。

$BC = AQ$

类似地，

$BCAP$是一个平行四边形。

$BC = AP$.....…(i)

$AQ = AP = BL$

这意味着，

$PQ = 2BC$

类似地，

$QR = 2AB$ 且 $PR = 2AC$

因此，

$\triangle PQR$的周长$= PQ + QR + PR$

$= 2AB + 2BC + 2AC$

$= 2(AB + BC + AC)$

$= 2 \times$ $\triangle ABC$的周长

证毕。

教程点

更新于: 2022年10月10日

43 次浏览

开启你的职业生涯

通过完成课程获得认证

开始学习