数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
时尚研究
法律研究在三角形ABC中，边AB、BC和中线AD分别与三角形PQR的边PQ、QR和中线PM成比例。证明三角形ABC相似于三角形PQR。
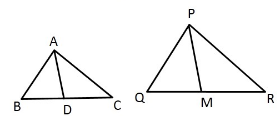
已知：两个三角形。ΔABC 和 ΔPQR，其中 ΔABC 的边 AB、BC 和中线 AD 与 ΔPQR 的边 PQ、QR 和中线 PM 成比例。
$\frac{AB}{PQ} = \frac{BC}{QR} = \frac{AD}{PM}$
证明：ΔABC ~ ΔPQR
解答
我们有 $\frac{AB}{PQ} = \frac{BC}{QR} = \frac{AD}{PM}$（D 是 BC 的中点，M 是 QR 的中点）
ΔABD ~ ΔPQM [SSS相似性准则]
因此，∠ABD = ∠PQM [两个相似三角形的对应角相等]
∠ABC = ∠PQR
在ΔABC 和 ΔPQR 中
$\frac{AB}{PQ} = \frac{BC}{QR}$ ———(i)
∠ABC = ∠PQR ——-(ii)
从以上公式 (i) 和 (ii)，我们得到
ΔABC ~ ΔPQR [根据SAS相似性准则]
更新于： 2022-10-10
107 次查看
广告