在三角形PQR中，如果PQ = QR，并且L、M和N分别是边PQ、QR和RP的中点。证明LN = MN。

已知

在三角形PQR中，PQ = QR，且L、M和N分别是边PQ、QR和RP的中点。

要求

我们必须证明LN = MN。

解答

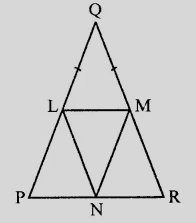
在三角形LPN和三角形MRH中，

PN = RN (因为M是PR的中点)

LP = MR

∠P = ∠R (等边对等角)

因此，根据SAS公理

三角形LPN ≅ 三角形MRH

这意味着，

LN = MN (全等三角形对应边相等)

证毕。

教程点

更新于: 2022年10月10日

96 次查看

开启你的职业生涯

通过完成课程获得认证

开始学习