M 和 N 分别是△PQR 的边 PQ 和 PR 上的点。对于以下每种情况，说明 MN 是否平行于 QR
PQ = 1.28 cm，PR = 2.56 cm，PM = 0.16 cm，PN = 0.32 cm

已知

PQ=1.28 cm，PR=2.56 cm，PM=0.16 cm 和 PN=0.32 cm。

要求

我们必须找到 MN 是否平行于 QR。

解答

我们知道，

如果一条直线将三角形的两条边按比例分割，则它平行于第三条边。


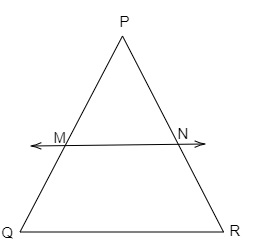
QM=PQ-PM=(1.28-0.16) cm=1.12 cm

NR=PR-PN=(2.56-0.32) cm=2.24 cm

因此，

PM/QM=0.16/1.12=0.16×100/1.12×100=16/112=1/7

PN/NR=0.32/2.24=0.32×100/2.24×100=32/224=1/7

PM/QM=PN/NR

因此，根据比例定理的逆定理，MN 平行于 QR。 

更新于： 2022年10月10日

54 次浏览

开启你的职业生涯

通过完成课程获得认证

开始学习
广告