作一个三角形$\mathrm{PQR}$，其中$\mathrm{QR}=6 \mathrm{~cm}，\angle \mathrm{Q}=60^{\circ}$且$\mathrm{PR}-\mathrm{PQ}=2 \mathrm{~cm}$。

已知

$QR=6\ cm, \angle Q=60^o$ 且 $PR-PQ=2\ cm$.

要求

我们需要作一个$\triangle PQR$。

解答

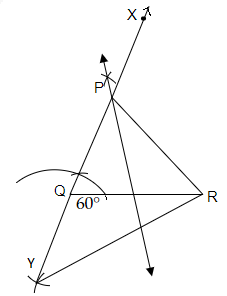
作图步骤

(i) 我们先画一条长度为 $6\ cm$ 的线段 $QR$。

(ii) 然后，作一个角 $RQX$，使得 $\angle RQX=60^o$

(iii) 现在，用圆规测量 $PR-PQ=2\ cm$，从点 $Q$ 画一个弧，并标记为点 $Y$。由于 $PQ-PR$ 为负，所以直线 $QY$ 将在线段 $QR$ 下方。

(v) 现在，用圆规从点 $Q$ 在 $QX$ 上画另一个弧。

(vi) 现在，连接 $YR$。然后用圆规作线段 $YR$ 的垂直平分线，并将平分线与射线 $QX$ 的交点标记为 $P$

(v) 现在，连接 $PR$。因此，$PQR$ 是所求的三角形。

教程点

更新于: 2022年10月10日

57 次浏览

开启你的职业生涯

通过完成课程获得认证

立即开始