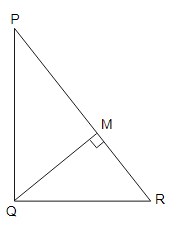
在三角形PQR中，PR² - PQ² = QR²，且M是边PR上的一点。
证明QM² = PM × MR。

已知

在三角形PQR中，PR² - PQ² = QR²，且M是边PR上的一点。

要求

我们需要证明QM² = PM × MR。

解答

PR² - PQ² = QR²

PR² = PQ² + QR²

这意味着：

△PQR是一个以Q为直角的直角三角形。

在△QMR和△PMQ中，

∠M = ∠M = 90°

∠MQR = ∠QPM = 90° - ∠R

因此，根据AA相似性，

△QMR ∽ △PMQ

利用相似三角形面积的性质，我们得到：ar(△QMR) / ar(△PMQ) = (QM)² / (PM)²

½ × RM × QM / ½ × PM × QM = (QM)² / (PM)²

QM² = PM × RM

证毕。

教程点

更新于：2022年10月10日

42 次浏览

开启你的职业生涯

通过完成课程获得认证

开始学习