在△PQR中，PD⊥QR，D在QR上。如果PQ=a，PR=b，QD=c，DR=d，证明(a+b)(a-b)=(c+d)(c-d)。

已知

在△PQR中，PD⊥QR，D在QR上。

PQ=a，PR=b，QD=c，DR=d

要求

我们必须证明(a+b)(a-b)=(c+d)(c-d)。

解答

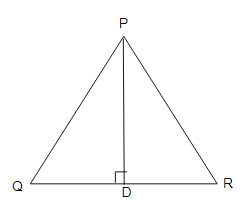
在直角三角形PDO中，

PQ²=PD²+QD²

a²=PD²+c²

PD²=a²-c²……(i)

在直角三角形PDR中，

PR²=PD²+DR²

b²=PD²+d²

PD²=b²-d²……(ii)

由(i)和(ii)，我们得到：

a²-c²=b²-d²

a²-b²=c²-d²

(a-b)(a+b)=(c-d)(c+d)

证毕。

教程点

更新于：2022年10月10日

64次浏览

开启你的职业生涯

完成课程获得认证

开始学习