数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学已知梯形\( \mathrm{ABCD} \)中，\( \mathrm{AB} \| \mathrm{DC} \)，点\( \mathrm{P} \)和\( \mathrm{Q} \)分别在\( \mathrm{AD} \)和\( \mathrm{BC} \)上，且\( P Q \| D C \)。如果\( P D=18 \mathrm{~cm} \)，\( B Q=35 \mathrm{~cm} \)和\( \mathrm{QC}=15 \mathrm{~cm} \)，求\( \mathrm{AD} \)的长度。
已知：
\( \mathrm{ABCD} \)是梯形，其中\( \mathrm{AB} \| \mathrm{DC} \)，\( \mathrm{P} \)和\( \mathrm{Q} \)分别是\( \mathrm{AD} \)和\( \mathrm{BC} \)上的点，且\( P Q \| D C \).
\( P D=18 \mathrm{~cm} \)，\( B Q=35 \mathrm{~cm} \) 和 \( \mathrm{QC}=15 \mathrm{~cm} \)
求解：
求\(AD\).
解
连接\(BD\)
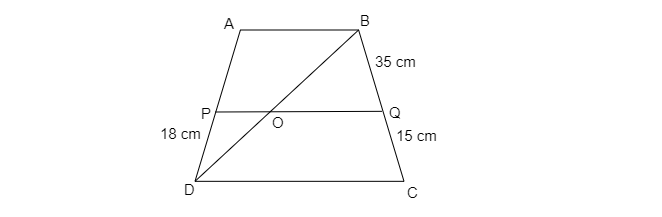
在\(\vartriangle ABD\)中，
\(PO \| AB\) [因为\(AB \| CD \| PQ\)]
因此，根据比例定理，
\(\Rightarrow \frac{DP}{AP}=\frac{DO}{OB}\)……(i)
在\(\vartriangle BDC\)中，
\(OQ \| DC\) [因为\(AB \| CD \| PQ\)]
因此，根据比例定理，
\(\frac{BQ}{QC}=\frac{OB}{OD}\)
\(\Rightarrow \frac{QC}{BQ}=\frac{OD}{OB}\)……(ii)
由(i)和(ii)可得，
\(\frac{DP}{AP}=\frac{QC}{BQ}\)
\(\Rightarrow \frac{18}{AP}=\frac{15}{35}\)
\(\Rightarrow AP=\frac{18\times 35}{15}\)
\(\Rightarrow AP=42\)
因此，
\(AD=AP+DP\)
$=42+18$
\(=60\ cm\)
更新于：2022年10月10日
68 次浏览
广告